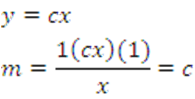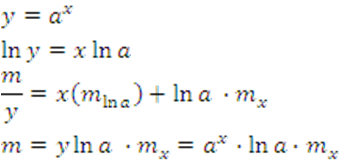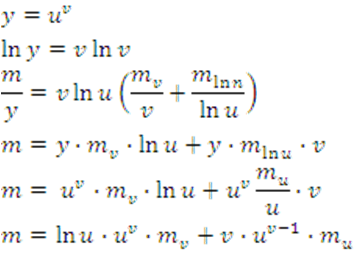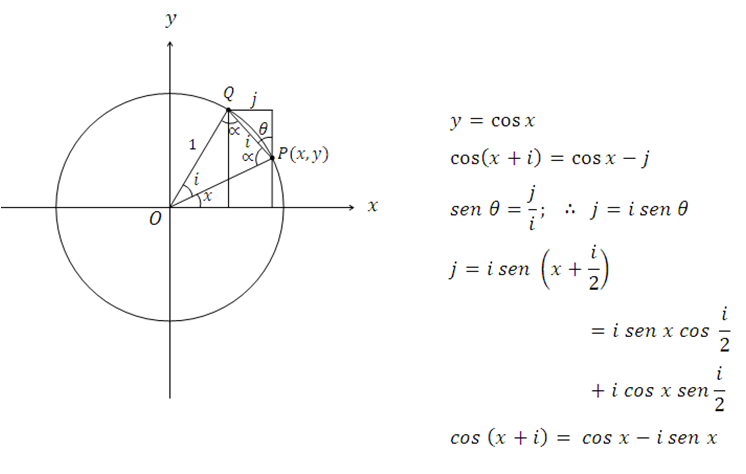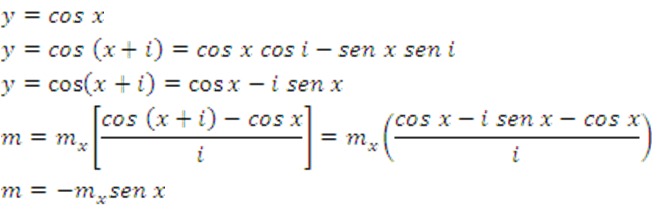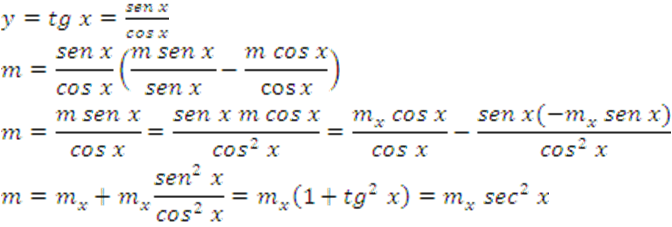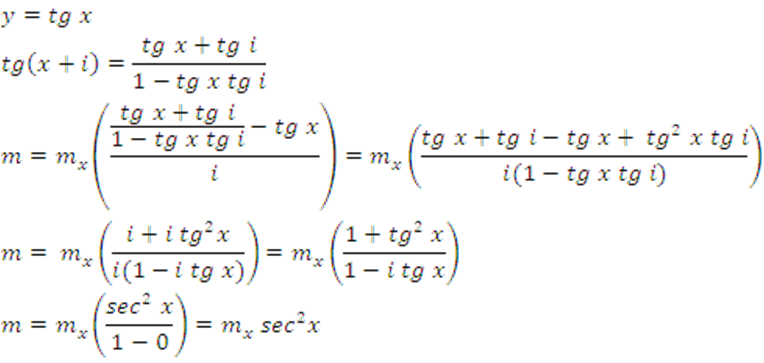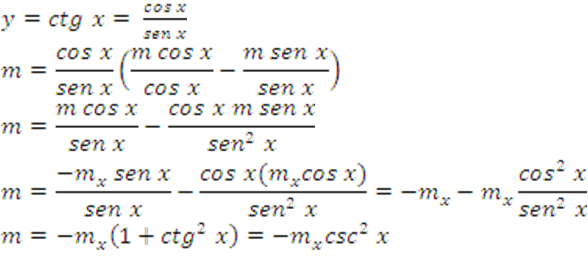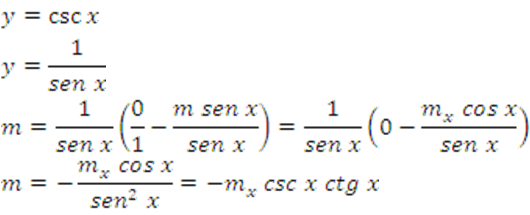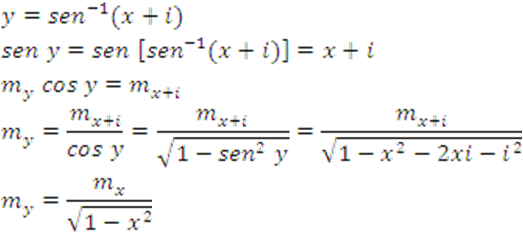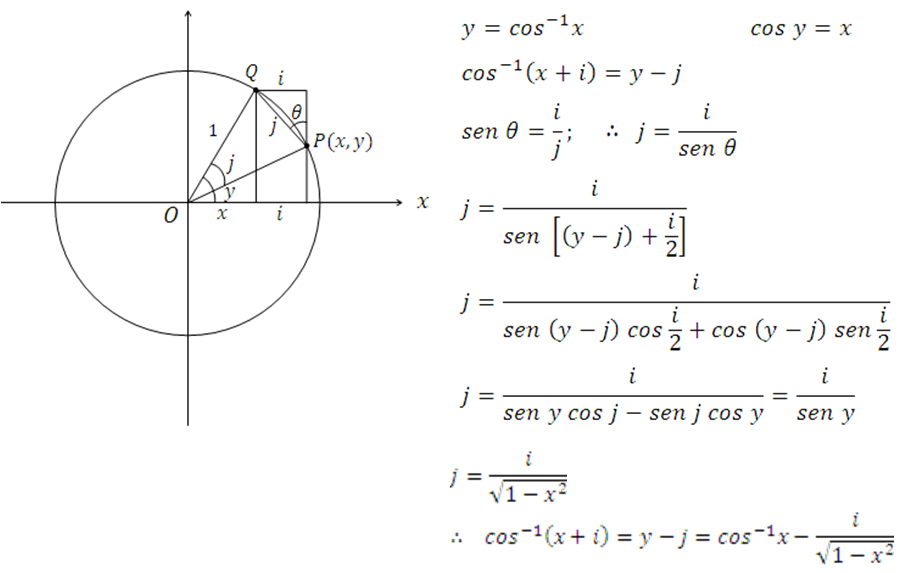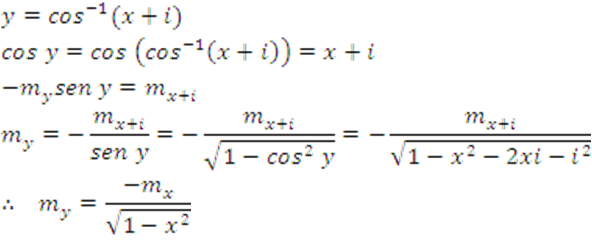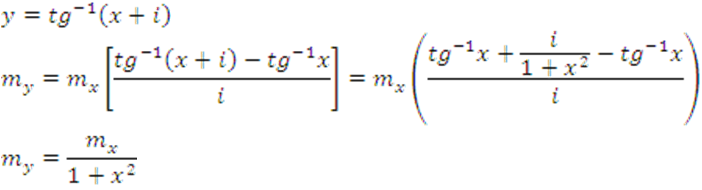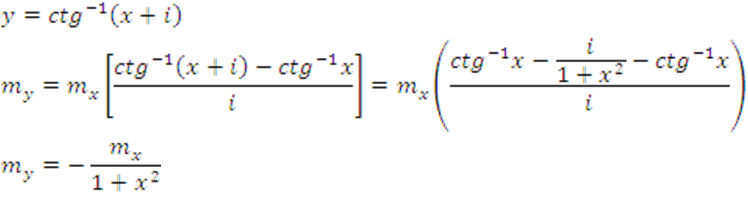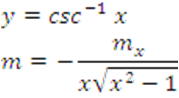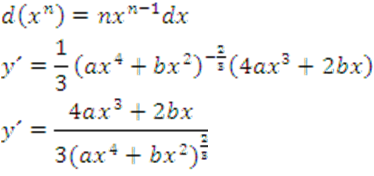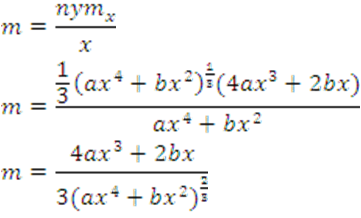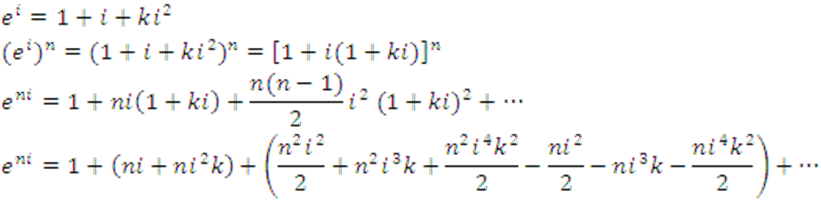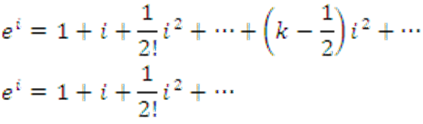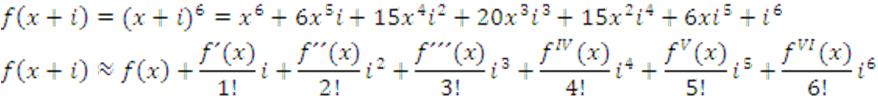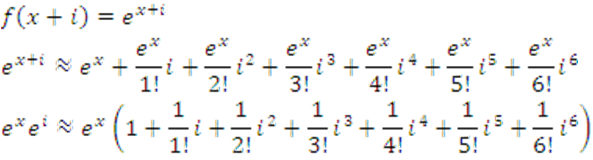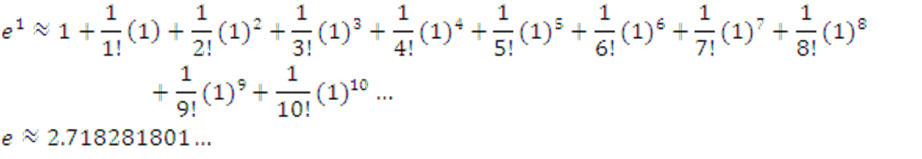Resumen

Este artículo pretende llamar la atención del número en cuanto a lo extremadamente pequeño y lo extremadamente grande con el fin de investigar más a fondo su naturaleza y aplicarlo a la solución de problemas utilizando esquemas diferentes.

El concepto de derivada usando el límite de la tangente ya no se utiliza; en cambio se trabaja con la secante y se obtiene una expresión general con la cual se llega a las reglas de derivación conocidas, evitando el salto de lo finito a lo infinito.

Palabras clave: nada, cero, infinito, límite, tangente, secante.

Abstract

This article is aimed to draw attention to the extremely small but at the same time big number which intends to find out its nature and property. It can be applied to the solution of problems using a wide range of schemes.

The concept of derivate using the tangent is not longer used. Now, the secant is used to obtain a general expression. This can lead to the known derivation rules, avoiding the leap from finite to infinite.

Keywords: nothing, zero, infinite, limit, tangent, secant.

Introducción

El número, como el tiempo, es absolutamente denso, no sabemos dónde principia ni dónde termina, por lo que no podemos aislarlo ni etiquetarlo; por lo tanto, la idea que tenemos como número: -3, -1, 0, 1, 5, π(Pi), e, 7, etcétera, no se puede sostener ya que no es digitalizado, es decir, no es una esferita, y, en esencia lo que conocemos como número 0 es sólo su aproximación: 0.00000000………1; lo mismo le sucede a cualquier otro número: 2.00000…………1.

Es curioso que a dos conceptos muy profundos como la nada y el infinito se les haya dado un tratamiento totalmente diferente; a la nada, el hombre le asigna un valor: el 0 y al infinito no le asigna ningún valor.

Al infinito lo simboliza como k/0 y se dice que la división entre 0 es la única operación imposible de la matemática.
Este cociente puede ser sustituido de la siguiente manera: k/i = I, donde i es extremadamente pequeño: i=0.0000000…….1, y a la I se le asigna un número extremadamente grande: I=9999999……99999.

Si aceptamos lo anterior los conceptos de continuidad, límite, tangentes, asíntotas, campos numéricos, convergencia, divergencia, formas indeterminadas, etcétera carecen de sentido.

También se cuestiona el carácter exacto de las matemáticas y sólo la consideraremos como una ciencia “precisa” y no exacta al igual que en la Física el movimiento perpetuo no existe y sólo se puede prolongar el mayor tiempo posible; en cuanto al número, también le podemos dar la aproximación que se quiera pero nunca se podrá llegar a la exactitud.

Utilizando lo anteriormente expuesto lo aplicaremos para dar una nueva visión al cálculo diferencial.

“Acercándonos a lo pequeño accedemos a lo grande, acercándonos a lo grande accedemos a lo pequeño”.
(Lerma D, 2013)

El concepto de límite y de finito

Constituye una gran confusión para el entendimiento de la Matemática Superior; desde hace siglos se debate sobre el tema y no hay una claridad en su razonamiento analítico, por tal razón sin necesidad del concepto de límite ni del infinito, es posible llegar a resultados exactos con tan solo tomar cantidades muy pequeñas cercanísimas al cero o muy grandes respecto al infinito y con ello llegar a lo mismo que el cero y el infinito logran pero haciendo uso de un “acto de fe” más que de un riguroso razonamiento.

Sirvan pues los siguientes cuestionamientos para evitar el Cálculo Diferencial y utilizar el Cálculo Pendiental.

Definición clásica de la derivada

Sea un punto sobre la gráfica y otro punto sobre . La pendiente de la recta que pasa por P y Q es:

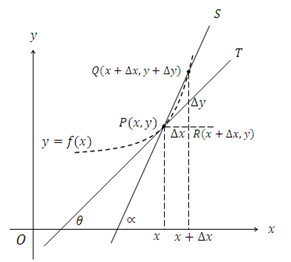
Si f(x) es una función definida en una vecindad de x, entonces la pendiente de T en el punto P obtenida mediante el siguiente límite, es lo que se conoce como la derivada de la función f(x) en el punto P:

La definición anterior no es nada clara ya que en el límite pueden ocurrir 3 casos:

a) Que ∆y llegue primero a cero, lo que nos daría

b) Que los 2 lleguen a cero al mismo tiempo

c) Y que ∆x llegue primero a cero

Éste último caso es el que se espera que ocurra y por fe aceptamos que el se convierta en la derivada.

Para evitar lo anterior y sin perder eficacia podemos considerar 2 cuestiones:

La secante nunca se convierte en la tangente, ya que al girar en torno al punto P, el punto Q se empalma con dicho punto P y sigue pasando por 2 puntos: P y Q (condición de secancia) y además la supuesta tangente también estaría pasando por P y Q violando la condición de que sólo toca un punto de la curva (tangencia), una tangente sólo corta a una curva en posición no paralela a un eje (en cierta vecindad).

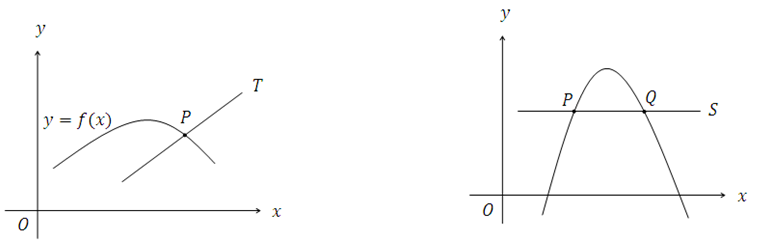
Ya que al ser paralela la cortaría en 2 puntos (al menos) la cual la convertiría en secante, condición que se puede aprovechar para extraer información de la función.

Se puede sustituir el concepto de derivada por el concepto de la pendiente de la secante que pasa por 2 puntos que tienen la misma ubicación en una vecindad de x, y con dicho concepto se obtienen todas las fórmulas de derivación, ahora denominadas fórmulas de pendientes. Lo cual evita la división entre cero.

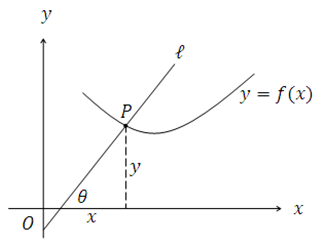
Del ángulo de inclinación de la recta , sabemos que la tangente de dicho ángulo es la pendiente de , por lo tanto , de donde . Si dicha pendiente m se multiplica por n, entonces se tiene el grado de inclinación de cierta pendiente y podemos generalizar , donde es la pendiente de la curva en el punto P(x,y), es la pendiente de la variable x.

De ahora en adelante la pendiente sustituye a la derivada, quitando la s simplemente queda:

Obtención de las fórmulas de derivación a través de la fórmula de las pendientes
c = constante

1.     2.      3.     4.

5.     6.      7.     8.

9.  

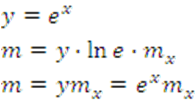
Regla de la Cadena

10.     11.     12.     13.

Como i es infinitamente pequeño: 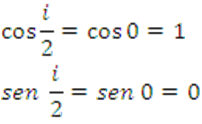También:

14. 14.

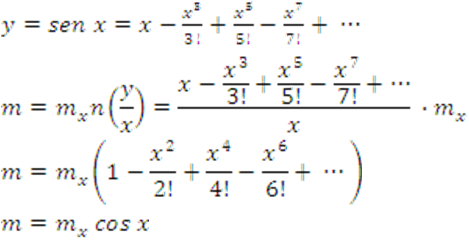
14.

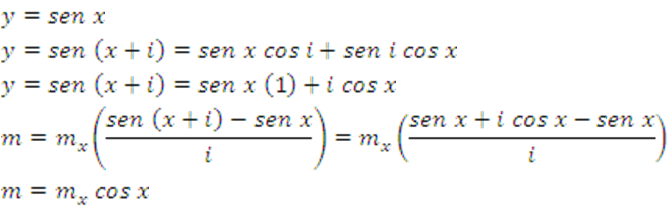
15. 15.

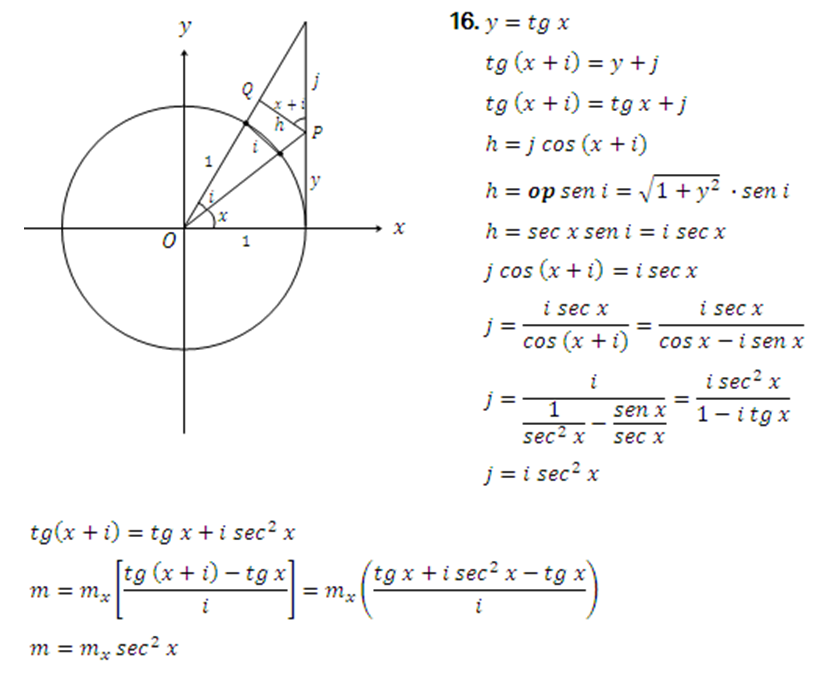
16.

16.

17.

18. 19.

 

20. 20.

21.

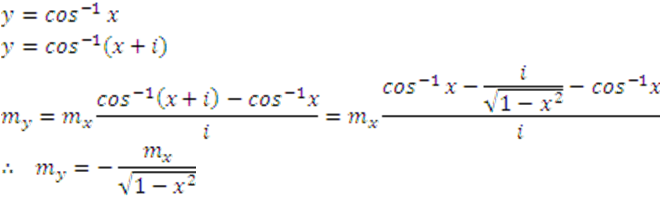
21. 21.

22.

22. 23.

23. 24. 25.

Ejemplo:

Sea

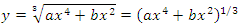
Usando la fórmula de la derivada de una potencia:

Usando la fórmula de las pendientes

Dos caminos para obtener el número e : y sea i=0.00000000000000………….1, entonces diferencia pequeñísima, ∴

Cambiando ni por Θ y reordenando términos, Y cambiando la θ muda por i,

Siguiendo el proceso se puede obtener, y para una mejor aproximación,

Por otro lado, Sea

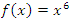
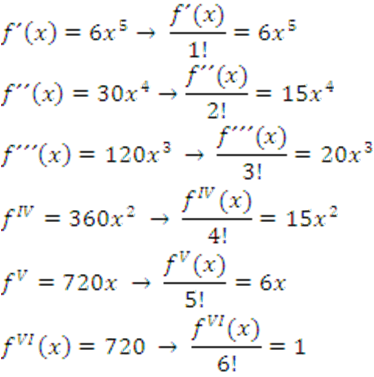
Si      

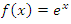
Por tanto

Y en general

Si x=1

Los resultados que se desprenden del análisis anterior constituyen una mejor comprensión de lo que se llama derivada y además termina con la “operación imposible” la división entre 0 y nos permite entender mejor la naturaleza del número acercándonos más a la realidad y alejándonos de la virtualidad y además termina con la creencia de que la matemática es una ciencia exacta y lo que este trabajo pretende aclarar es que la matemática es una ciencia precisa y que la exactitud no existe.

Referencias

1. Carreón M., Vicente, Módulo de Hiperreales, Sección Matemática Educativa del Centro de Investigación y Estudios Avanzados del I.P.N. (1984).
2. Leithold, Louis, Cálculo con Geometría Analítica. Editorial Harla. (1994).
3. Earl W. Swokowski, Cálculo con Geometría Analítica. Grupo Editorial Iberoamericana. (1998).
4. Zill, Denis G. Cálculo con Geometría Analítica, Grupo Editorial Iberoamericana. (1987).
5. Wesley, Addison, Apostol T.M., Análisis Matemático, Reading, Mass. (1974).
6. Barthe, Robert G., Introducción al Análisis Matemático, Quinta Edición. (1991).
7. Rivera Antonio, Análisis I y II, Sección Matemática Educativa del Centro de Investigación y Estudios Avanzados del I.P.N. (1984).
8. Boltiansky, V.G., Qué es Cálculo? Lecciones Populares de Matemáticas. Editorial MIR. Moscú. Tercera Edición. (1984).
9. Nikolsky, S.M., Elementos de Análisis Matemático, Editorial MIR. Moscú. (1984).
10. Olea Franco, Pedro, Manual de Técnicas de Investigación documental. Editorial Esfinge S. A. (1985).