Año 3, Número 2. Enero - Abril 2016 
Algoritmo genético y algoritmo de sistema de hormigas aplicados al problema del agente viajero
Genetic algorithm and applied ant system algorithm to the traveling agent problem
Instituto Tecnológico de León
Por: Uriel Ervey Bernal Magallanes, Héctor José Puga Soberanes y Juan Adolfo Montesino Guerra / Ver en pantalla completa
Resumen
El Problema del Agente Viajero (por sus siglas en ingles TSP) es un problema clásico ampliamente estudiado dentro del área de optimización combinatoria. Hasta la fecha no se ha encontrado un algoritmo exacto que encuentre la solución óptima a este problema en un tiempo polinomial. El algoritmo Genético (AG) y el Algoritmo de sistema de Hormigas (ASH) son dos metaheurísticas, las cuales han reportado en el estado del arte buenas soluciones aproximadas a problemas de optimización combinatoria. El objetivo de este trabajo es mostrar la implementación y el funcionamiento de un AG y del ASH aplicado al TSP simétrico, mostrando los resultados obtenidos durante la experimentación.
Palabras Clave: Problema del Agente Viajero (TSP), metaheurísticas, Algoritmo Genético, Algoritmo de Sistema de Hormigas.
Abstract
The Traveling Salesman Problem (TSP) is a classic problem of the area of combinatorial optimization. An exact algorithm that solves this problem in polynomial time has not been found. The Genetic Algorithm (GA) and Ant System Algorithm (ASA) are two Metaheuristics which have reported approximate good solutions to combinatorial optimization problems. The goal of this work is to show the implementation and performance of a GA and ASA applied to symmetrical TSP, showing the results obtained during experimentation.
Keywords: Traveling Salesman Problem (TSP), Metaheuristics, Genetic Algorithm, Ant System Algorithm.
Introducción
El problema del agente viajero o TSP es un problema que pertenece a la clase de problemas NP-Duros debido a que no existe un algoritmo exacto que lo resuelva en tiempo polinomial. La supercomputadora RoadRunner del departamento de energía de los estados unidos, la cual en el 2009 encabezo el ranking de las 500 supercomputadoras más rápidas del mundo, con un total de 129,600 núcleos y una capacidad de procesamiento de 1.457 trillones de operaciones aritméticas por segundo, tardaría 28 trillones de años en resolver una instancia del TSP de 33 ciudades, utilizando como método la búsqueda exhaustiva1. La importancia del TSP se estriba en que varios problemas de optimización combinatoria se pueden modelar con base en él, como la planeación de rutas de transporte, el taladrado en placas de circuitos, la planeación de tiempos de vuelos y la asignación de tareas, así como otros que pueden ser consultados1. Existen métodos conocidos como Metaheurísticas los cuales son algoritmos aproximados que se pueden adaptar a varios problemas de optimización2. Las Metaheurísticas no prometen encontrar la solución óptima pero si una solución aproximada en un tiempo factible3. El AG y el ASH son dos Metaheurísticas populares que han tenido éxito en encontrar soluciones aproximadas a problemas de optimización combinatoria.
Conceptos teóricos
Problema de Agente Viajero (TSP)
La primera formulación del TSP fue entre 1920 y 1930, por el matemático y economista Karl Menger1.
El TSP se puede plantear de la siguiente manera dado un conjunto de n ciudades V={1,2,3,…n} y un conjunto de aristas A={ (i,j) | i,j ∈ V} que interconecta las ciudades, encontrar la ruta o el recorrido de costo mínimo que recorra todas las ciudades una sola vez partiendo de una ciudad inicial y terminando en esa misma ciudad inicial. A este tipo de recorrido se le conoce como ciclo hamiltoniano.
El modelo del TSP se puede plantear de la siguiente forma4:
(1.1)
Sujeto a:
(1.2)
(1.3)
(1.4)
De donde:
- A⊆V×V es el conjunto de las aristas que interconectan las ciudades.
- xij es la variable de decisión del problema que está dada por:
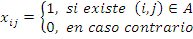 (1.5)
(1.5)- Cij es el costo o la distancia asociado a xij.
La expresión (1.1) representa la función objetivo a minimizar, la restricción (1.2) indica que para cada ciudad j que no ha sido visitada se puede llegar a ella solo de una ciudad i, la restricción (1.3) indica que para cada ciudad i solo puede llegar a una sola ciudad j la restricción (1.4) evita que se generen subtours.
Existen dos versiones del TSP:
- TSP simétrico, cuando ∀ (i,j)∈A,Cij=Cji.
- TSP asimétrico, cuando ∀ (i,j)∈A ∃ (i,j),Cij≠Cji.
Algoritmo Genético (AG)
Los algoritmos genéticos (AGs) son una clase de metaheurísticas muy populares pertenecientes a la familia de Algoritmos Evolutivos, fueron propuestos por John Holland en la Universidad de Michigan, alrededor de 19705. Los AGs son algoritmos de optimización basados en la teoría de la selección natural, la evolución y la genética6. Un AG consta de los siguientes elementos para su funcionamiento:
- Una población P inicial de n individuos, donde cada individuo es una solución.
- Una Función objetivo f conocida como función de fitness o simplemente fitness, la cual evaluará la calidad del individuo.
- Una codificación de individuo, la cual permitirá adaptar las posibles soluciones al dominio del problema.
También consta de los siguientes operadores:
- Selección: Este operador selecciona los individuos que se van a reproducir en base a su función de fitness.
- Cruza: Este operador realiza un intercambio de genes entre dos individuos seleccionados.
- Mutación: Modifica el material genético de un individuo de manera aleatoria.
Se muestra el funcionamiento del AG aplicado al TSP, y el orden en el que se tienen que aplicar los operadores:
Codificación de permutación
En este tipo de codificación cada individuo es representado por una permutación (a1,a2,a3,…,an) tal que a1,a2,a3,…,an ∈N. La permutación (a1,a2,a3,…,an) representa la ruta en el orden que se tienen visitar las ciudades. Donde a1,a2,a3,…,an son las ciudades que se tienen que visitar.
Selección por torneo
Este operador consiste en seleccionar k individuos aleatoriamente para competir en un torneo. El ganador del torneo es aquel individuo con mejor fittness. Este proceso se repite l veces, donde l es el tamaño de la población P. Para el TSP, el AG utiliza como función de fittness a (1.1).
Cruza: Order Crossover (OX)
Este operador consiste en el intercambio genético de dos parientes para generar dos nuevos hijos. Se muestra el siguiente ejemplo para mostrar su funcionamiento:
Se selecciona una parte del padre P1 y se agrega al hijo H1. Se hace lo mismo para P2 y H2.
P1=(1,2,3,5,4) P2=(3,4,1,5,2)
H1=(-,2,3,5,-) H2=(-,4,1,5,-)
Después los espacios faltantes en H1 se rellenan con los elementos de P2 que no estén en H1. Se hace lo mismo para H2 con P2.
H1=(4,2,3,5,1) H2=(2,4,1,5,3)
Mutación: Swap-Two
La mutación de Swap-Two consiste en seleccionar un individuo i ∈P de manera aleatoria. Después seleccionar dos componentes c1 y c2 de i e intercambiarlos entre ellos. Se muestra el funcionamiento de Swap-Two con el siguiente ejemplo:
Sea i=(1,2,3,4,5), c1=3 y c2=5.
Aplicando el operador de mutación de Swap-Two obtendríamos:
i=(1,2,5,4,3)
Existen diferentes tipos de codificación, selección, cruza y mutación los cuales pueden consultarse en Dumitrescu y otros7. Se muestra en la figura 1 pseudocodigo del AG:
Algoritmo Genético
Asignar e inicializar parámetros
Mientras (La condición de paro no se satisfaga) hacer
Aplicar_elitismo %opcional
Aplicar_Selección
Aplicar_Cruza
Aplicar_MutaciónEnd
Figura 1. Pseudocódigo del AG
Algoritmo de Sistema de Hormigas (ASH)
El ASH es un algoritmo que fue propuesto en 1991 por Marco Dorigo8. En un principio se crearon tres versiones del algoritmo llamadas ant-density, ant-quantity, y ant-cycle8. Hoy en día, el ASH se refiere al ant-cycle debido a que las otras dos versiones fueron abandonadas debido a su inferior rendimiento. Esta metaheurística está inspirada en el comportamiento de las hormigas reales.
Las hormigas son capaces de encontrar la ruta más corta entre la colonia y una fuente de comida. En un principio cada hormiga va construyendo un camino aleatoriamente y durante el transcurso va depositando una cantidad de feromonas. Las hormigas utilizan las feromonas para seleccionar un camino, lo cual quiere decir que una hormiga seleccionará el camino donde haya una mayor concentración de feromonas. Las feromonas tienden a evaporarse y desaparecer con el tiempo, por lo tanto, la concentración de feromonas en las rutas de mayor longitud tiende a desaparecer más rápido que la concentración de feromonas de las rutas de menor longitud.
Se muestra el funcionamiento del ASH aplicado al TSP:
En el ASH, cada hormiga artificial k construye una solución, iniciando aleatoriamente de una ciudad i, para ir de i a j una hormiga selecciona un camino en base a la probabilidad, la cual está dada por (2.1):
(2.1)
De donde:
-
τij es la cantidad de feromona del arco (i,j).
-
ηij es la información heurística la cual está dada por ηij=
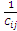
-
cij es el costo o distancia del arco.
-
α es la influencia relativa de la feromona.
-
β es la influencia relativa de la información heurística.
-
Nik es el vecindario de ciudades no visitadas de i.
Después de que todas las han construido una solución, lo siguiente es actualizar los valores de las feromonas que están sobre los arcos. Esta actualización está dada por la ecuación (2.2):
(2.2)
De donde:
- ρ es el porcentaje de evaporación de las feromonas.
- Δτijk es el incremento de la feromona en el arco (i,j), realizado por la hormiga k.
(2.3)
- Ck es el costo o la longitud del tour Tk , realizado por la hormiga k.
Existen más variedades sobre el ASH las cuales pueden consultarse en Dorigo y otros8. Se muestra en la figura 2 el pseudocodigo del ASH:
Algoritmo de Sistema de Hormigas
Asignar e inicializar parámetros
Mientras (La condición de paro no se satisfaga) hacer
Construir_Soluciones_de_hormigas
Aplicar_busqueda_local %opcional
Actualizar_feromonasEnd
Figura 2. Pseudocódigo del ASH.
Experimentación
Se utilizó el lenguaje de programación Java para la implementación de los algoritmos.
Para probar el funcionamiento de los algoritmos se utilizaron las siguientes instancias de prueba de caso simétrico (KroA100, KroB100, KroC100, KroA150, KroB150, KroC150, KroA200, KroB200, KroC200, A280).Estas instancias fueron obtenidas de G .Reinelt9.Como condición de paro se usó el criterio de “número de llamadas a función”, se utilizó a (1.1) como función objetivo a minimizar. En cada ejecución del algoritmo, se obtuvo la solución con menor distancia.
Para realizar las pruebas se utilizó un equipo de cómputo Acer E5-411 con las siguientes características:
- Procesador: Intel Celeron Processor N2830 de 2.16 GHz.
- Memoria RAM: 4 GB.
- Sistema Operativo: Windows 8.1, de 64 bits.
Se puede ver en la tabla 1 y 2 la configuración de parámetros para el AG y el ASH.
| Parámetros | Valores |
|---|---|
| Población | 33 |
| N° de llamadas a función | 1,000,000 |
| Porcentaje de Elitismo | 10% |
| Probabilidad de cruza | 1 |
| Probabilidad de muta | 1 |
Tabla 1. Configuración de parámetros para el AG.
| Parámetros | Valores |
|---|---|
| Población | 33 |
| N° de llamadas a función | 10,000 |
| Matriz τij | u~(0,0.3), u es aleatorio |
| Influencia relativa de la feromona ( α ) | 1 |
| Influencia relativa de la información heurística ( β ) | 2 |
| Coeficiente de evaporación | 50% |
Tabla 2. Configuración de parámetros para el AS
Resultados
Se muestran los resultados obtenidos durante la experimentación en la tabla 3.
| Instancias | Óptimo Conocido | AG | ASH |
|---|---|---|---|
| KroA100 | 21282 | 41996.148 | 24683.881 |
| KroB100 | 22141 | 39771.65 | 24179.582 |
| KroC100 | 20749 | 43369.454 | 21799.108 |
| KroD100 | 21294 | 37951.798 | 23567.693 |
| KroE100 | 22068 | 35982.682 | 24354.761 |
| Pr124 | 59030 | 153643.696 | 63500.17 |
| KroA150 | 26524 | 56839.17 | 30503.87 |
| KroB150 | 26130 | 63819.041 | 29875.772 |
| KroA200 | 29368 | 84105.103 | 38736.861 |
| KroB200 | 29437 | 77528.39 | 34958.148 |
Tabla 3. Resultados obtenidos del AG y el ASH.
Se muestra en la tabla 4 el tiempo de ejecución de los algoritmos para cada instancia de prueba durante la experimentación en minutos.
Instancias |
Tiempo de ejecución con AG |
Tiempo de ejecución con ASH |
| KroA100 | 0.0629 | 0.3176 |
| KroB100 | 0.0641 | 0.3180 |
| KroC100 | 0.0628 | 0.3116 |
| KroD100 | 0.0647 | 0.3143 |
| KroE100 | 0.0637 | 0.3149 |
| Pr124 | 0.0778 | 0.5941 |
| KroA150 | 0.1082 | 1.0265 |
| KroB150 | 0.1076 | 1.0274 |
| KroA200 | 0.2104 | 2.4417 |
| KroB200 | 0.2090 | 2.4527 |
Tabla 4. Tiempo de ejecución del AG y el ASH.
Conclusión
En este trabajo se mostró la implementación y el funcionamiento del AG y del ASH para la búsqueda de soluciones aproximadas al TSP. En la tabla 3 se puede observar los resultados obtenidos de la implementación del AG y el ASH para instancias de 100, 124,150 y 200 ciudades, donde se puede apreciar que estos algoritmos ofrecen soluciones aproximadas en una cantidad de tiempo razonable comparada con el método de búsqueda exhaustiva. En esta implementación se observa que el ASH obtuvo mejores soluciones aproximadas al óptimo que el AG, para todas las instancias utilizadas con una cantidad menor de llamadas a función. Sin embargo no es posible afirmar que el ASH es mejor que el AG debido que para realizar una comparación entre Metaheurísticas se requiere que los algoritmos tengan las mismas condiciones referente al tamaño de la población y a la cantidad de llamadas a función así como un procedimiento formal estadístico a priori10.
Agradecimientos
Los autores agradecen al Tecnológico Nacional de México-Instituto Tecnológico de León, que a través de la División de Estudios de Posgrado e Investigación (DEPI) dieron su apoyo para la realización del presente proyecto.
Referencias
1. WILLIAM J. Cook. In Pursit of the Traveling Salesman Mathematics at the Limits of Computation. New Jersey : Princeton University Press, 2012. ISBN 978-0-691-15270-7.
2. FRED, Glover y A. Kochenberger, Gary. HandBook of Metaheuristics. New York : Kluwer Academic Publishers, 2003. ISBN 1-4020-7263-5.
3. EL-GHAZALI, Talbi. Metaheuristics from design to implementation. Hoboken, New Jersey: John Wiley, 2009. ISBN 978-0-470-27858-1.
4. MONTESINO GUERRA, Juan Adolfo; PUGA SOBERANES, Héctor José; ORNELAS RODRIGUEZ, Manuel; CARPIO VALADEZ, Juan Martín; BERNAL MAGALLANES, Uriel Ervey. 2015. Análisis Comparativo de Metaheurísticas Aplicadas al Problema del TSP. León Guanajuato: XII encuentro Participación de la Mujer en la Ciencia.
5. MITCHELL, Melanie. An Introduction to Genetic Algorithms. Cambridge, Massachusetts : The MIT Press, 1998. ISBN 0−262−13316−4 (HB), 0−262−63185−7 (PB).
6. F. Luger George. Artificial Intelligence Structures and Strategy for Complex Problem Solving. New York : Pearson Addison Weasley, 2009. ISBN-13: 978-0-321-54589-3.
7. DUMITRESCU, D. y otros. Evolutionary Computation. Florida : CRC Press, 2000. ISBN 0-8493-0588-8.
8. DORIGO, Marco y STÜTZLE, Thomas. Ant Colony Optimization. Cambridge, Massachusetts : The MIT Press, 2004. ISBN 0-262-04219-3.
9. REINELT, Gerhard.TSPLIB 95. 1995, Universität Heidelberg, p. 1-17.
10. DERRAC, J., GARCÍA, S., MOLINA, D., HERRERA, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm and Evolutionary Computation, 2011, 1(1), 3-18.



