Año 6, Número 3. Mayo - Agosto 2019 
Análisis comparativo de cinco configuraciones geométricas de juntas soldadas en filetes sometidas a tensión
Comparative analysis of five geometric configurations of soldered joints in fillets subjected to tension
Instituto Tecnológico de Ciudad Guzmán / Instituto Tecnológico José Mario Molina Pasquel y Henríquez Campus Tamazula
Por: Elías Sánchez Montaño, Cesar Alejandro Cueto García, Luis Gabriel González Vázquez y Víctor Rafael Catzim Serra / Ver en pantalla completa
Resumen
Esta investigación aporta los resultados de los análisis matemáticos realizados a los cinco casos más comunes de soldadura de placas en filete. Los modelos matemáticos fueron determinados de forma algebraica, se consideró conocido el espesor de la solera y el tipo de electrodo, y a partir de estos datos se determinó la fuerza de fluencia y última de tracción para cada caso. Con los modelos matemáticos se elaboraron las tablas, con las cuales, si se conoce la carga que soportará una estructura, se puede seleccionar el espesor adecuado de la solera y el tipo de electrodo más conveniente a utilizar. La bondad de este trabajo radica en que esta información puede ser empleada con facilidad por los técnicos soldadores.
Palabras Clave: Soldadura, configuración geométrica, fuerza de fluencia, electrodo.
Abstract
This research provides the results of the mathematical analysis, made to the five most recurrent cases in plates welded in fillet. The mathematical models were deduced in an algebraic way, starting from the fact that the thickness of the hearth, the type of electrode, is known and with these data it is sought to determine the creep force and ultimate tensile force, both for each particular arrangement. Mention that with the mathematical models were made tables in which; if you know the load that supports the element, you can select the appropriate thickness of the hearth and the most convenient type of electrode to use. The goodness of this work lies in the fact that this information can be used easily by the welding technicians.
Keywords: Welding, geometric configuration, creep strength, electrode.
Introducción
De acuerdo con Rodríguez1, el término soldadura lo podemos definir como “la unión mecánicamente resistente de dos o más piezas metálicas diferentes”. La información relacionada con la configuración geométrica empleada en juntas soldadas es insuficiente, por esa razón se ha buscado investigar este tema. Sin embargo, es complejo analizarlo por las diversas consideraciones que se dan entre la unión de las placas a soldar, como sería; la distribución del campo vectorial de esfuerzos generados dentro del cordón. Molera2 menciona: “Desde antiguo se ha venido cumpliendo el aforismo que reza soldar es bueno, pero no soldar es mejor”.
Se seleccionaron cinco casos de estudio comunes, comparando la longitud de cordón, fuerza ultima de tracción y de fluencia al utilizar diferentes espesores de placas y de electrodos. La información que se generó se concentró en tablas de resultados. La nomenclatura utilizada en la soldadura con filetes transversales se ilustra en la Figura 1, donde F simboliza la fuerza aplicada, h el espesor de la solera y la sección ABCD representa la región transversal de la soldadura.
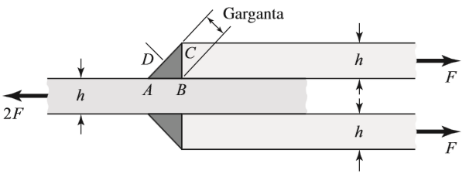
Figura 1. Soldadura con filetes transversales. Fuente de consulta: Boudynas y Nisbett6.
También se analizaron las gráficas de Norris3 (1945) y Salakian4 (1937), para tener una idea de cómo es la distribución del esfuerzo en la soldadura de filete (ver la Figura 2).
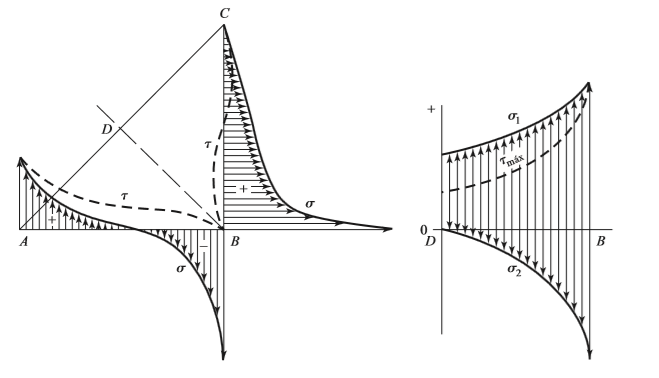
Figura 2. Gráficas de los resultados obtenidos por Norris (Izquierda) y Salakian (derecha), respecto a sus investigaciones. Fuente de consulta: Boudynas y Nisbett6
En la Figura 2 se observó que hay una concentración de esfuerzos en el punto B, en el que los esfuerzos componentes generados por el corte oblicuo D – B (Figura 1, en la sección de la garganta; normal y cortante) son graficados para el material de aporte (la soldadura). Esto nos llevó a realizar, como tercera actividad, deducir un modelo matemático sencillo que describiera el comportamiento del esfuerzo para cada caso.
Objetivo
Estudiar los cinco casos más recurrentes de soldadura en filete simétrica y tabular los resultados obtenidos del análisis teórico.
Planteamiento del problema
La configuración geométrica de un cuerpo sometido a fuerzas de cualquier tipo es determinante en lo que respecta a la funcionalidad para la cual fue diseñada. Como ejemplo, considere que, al colocar una barra de acero con sección transversal rectangular como viga, y colocarle una carga puntual y constante, la deflexión que esta sufra estará en función de la orientación que le demos (momento de inercia de la sección) a la propia sección transversal. Así pues: ¿qué sucede con la distribución geométrica de las juntas soldadas en filete?
El problema que se resolvió trata de la dispersión de información práctica referente al análisis teórico de geometrías de arreglos soldados sometidos a esfuerzos cortantes “internamente”, sin modificar las propiedades metalúrgicas de la soldadura ni del soporte, solo modificando aspectos geométricos y de orientación de la soldadura.
Método de trabajo
Se realizó una deducción de los modelos matemáticos para cada caso de forma algebraica, como se muestra a continuación:
Al hacer un corte oblicuo (Figura 4) al perfil del filete (Figura 1) D – B, en un caso teórico en el que tengamos dos ángulos de 45°, y denominamos a la garganta como t y los catetos del filete como h; podemos usar la teoría de senos para encontrar t en función de h. Esto debido a que en campo no resulta muy práctico hacer la medición de la garganta, es mucho más sencillo hacer la medición de los catetos, entonces tenemos:
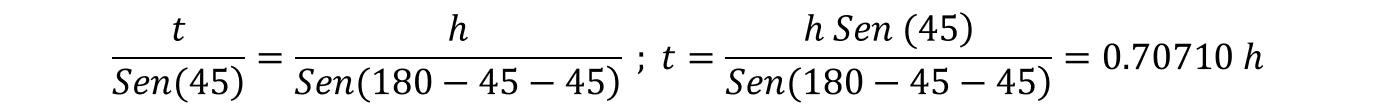 (1)
(1)
Al hacer el corte de la sección, se generan automáticamente dos fuerzas: una normal a la sección de corte oblicuo y otra cortante, paralela a la misma sección. En la Figura 3 se ilustra el diagrama de cuerpo libre, que nos sirve para describir de manera visual las características vectoriales de las fuerzas que interactúan entre sí.
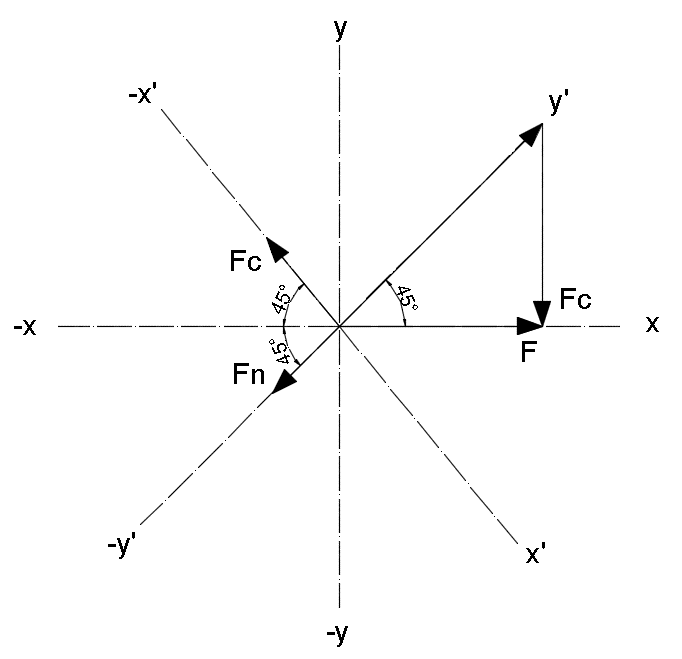
Figura 3. Diagrama de cuerpo libre, con traslación de ejes a x’ ý y’ Fuente de consulta: autoría propia.
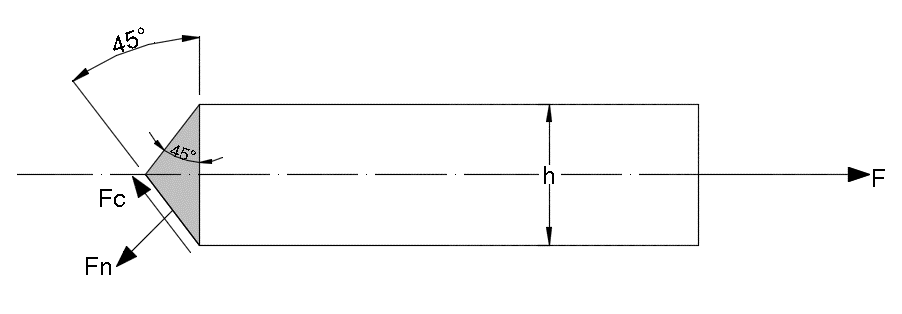
Figura 4. Corte oblicuo en la parte superior del arreglo soldado. Fuente de consulta: autoría propia.
Para determinar la magnitud de las fuerzas Fc y Fn, se define que el plano sobre el que trabajamos es el x’ y el y’, esto con la finalidad de simplificar los cálculos.
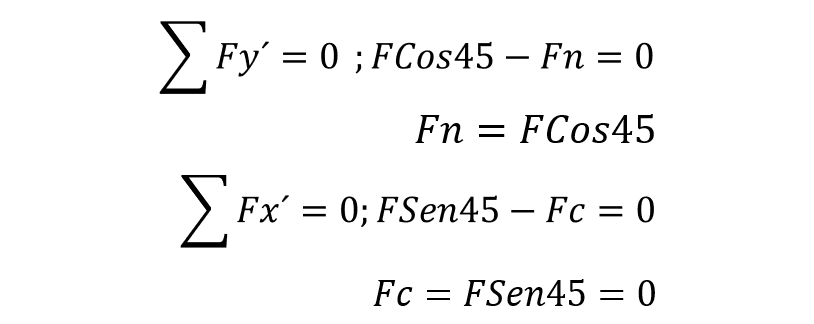 |
(2) |
| (3) | |
| (4) | |
| (5) |
Teniendo las ecuaciones (3), (5) y (1), y considerando que ambas fuerzas (normal y cortante) se aplican sobre el área de corte oblicuo; se determinaron los respectivos esfuerzos, obteniéndose que el esfuerzo normal es:
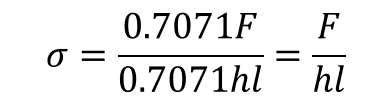 (6)
(6)
Y el esfuerzo cortante es:
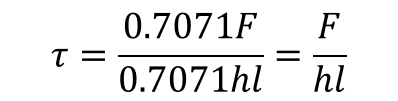 (7)
(7)
A partir de las ecuaciones (6) y (7) se estableció un estado general de esfuerzos para el esfuerzo normal σ y el cortante oblicuo τ, como se observa en la Figura 5.
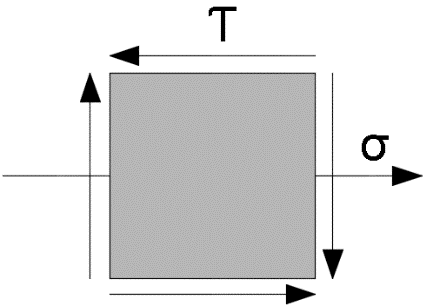
Figura 5. Representación del elemento diferencial sometido a esfuerzos. Fuente de consulta: autoría propia.
Se desarrolla el cálculo de los esfuerzos principales para esta transformación de esfuerzos5.
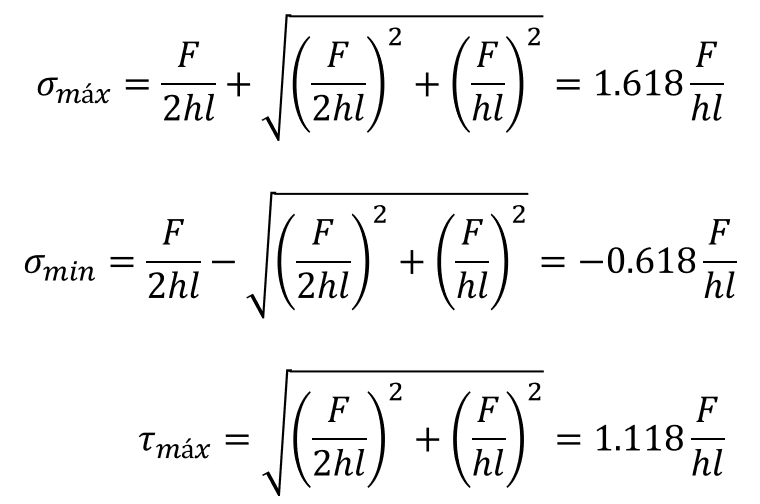 |
|
(9) |
|
(10) |
Los ángulos a los que se encuentran los esfuerzos principales antes calculados, mediante las ecuaciones5 apropiadas:
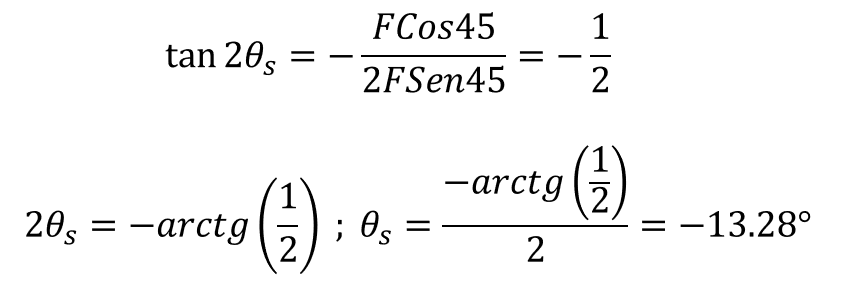 |
(11) |
(12) |
El ángulo θs representa la posición en la cual el esfuerzo principal de cortante máximo se encuentra.
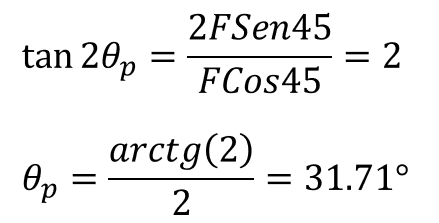 |
(13) |
(14) |
El ángulo θp representa la posición en la cual los esfuerzos principales normales se encuentran. Con todo lo anterior se estableció la solución del estado general de esfuerzos para un corte oblicuo a 45° grados en la soldadura de filete, presentado en la Figura 6.
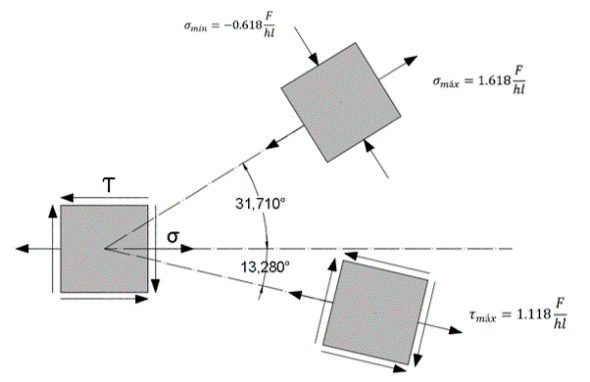
Figura 6. Solución del estado general de esfuerzos. Fuente de consulta: autoría propia.
El análisis sugirió que en el punto analizado a 45° en el corte oblicuo presentado por la Figura 6, la dirección del esfuerzo normal está ubicada a 31.710°. Mientras que la del esfuerzo cortante está ubicada a -13.280°, ambos con respecto a nuestro plano x’ ý y’.
El esfuerzo de mayor magnitud es el presentado por la ecuación (8). Lo que nos lleva a ser más conservadores en este aspecto, y siguiendo con lo propuesto por Boudynas y Nisbett6 tomamos como despreciable el esfuerzo normal, suponiendo de esta manera que el único esfuerzo al que está sometida la garganta es a un esfuerzo de cortante puro, por lo tanto:
![]() (15)
(15)
Resultados
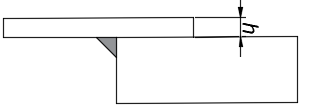
CASO 01: Se considera un solo cordón de soldadura en un lado de la parte trasera de la solera;
| a) Vista superior | b) Vista isométrica |
 |
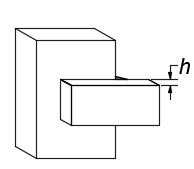 |
Figura 7. Vistas de la soldadura para el caso 01: a) superior, y b) isométrica Fuente de consulta: autoría propia.
El esfuerzo cortante se determinó mediante la ecuación (16):
![]() (16)
(16)
El área es igual al producto entre la longitud de la garganta y la longitud del cordón:
![]() (17)
(17)
Ahora, si consideramos la longitud de la garganta en función del ancho de solera h, en la ecuación (1), entonces el esfuerzo se reescribe como:
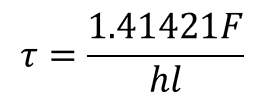 (18)
(18)
En la ecuación (18), se despeja la longitud (19) y la fuerza (20), obteniéndose:
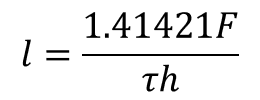 (19)
(19)
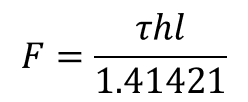 (20)
(20)
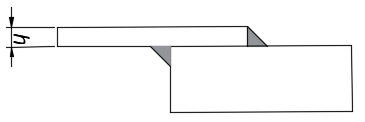
CASO 02: Tiene similitudes con el caso 01, solo que con dos cordones paralelos.
| a) Frontal | b) Isométrico |
 |
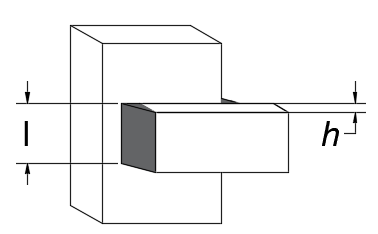 |
Figura 8. Vistas de la soldadura para el caso 02: a) superior, y b) isométrica Fuente de consulta: autoría propia.
En este caso número 02, lo único que cambió con respecto al caso número 01 fue la longitud del cordón, que es dos veces la de un solo cordón, entonces;
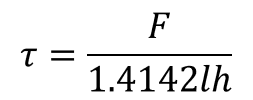 (21)
(21)
Enseguida, al igual que en el caso 01, despejamos la longitud (ecuación 22) de cada cordón y la fuerza (ecuación 23):
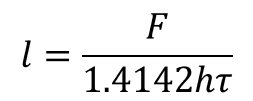 (22)
(22)
![]() (23)
(23)
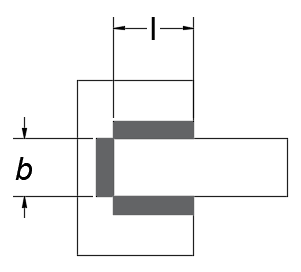
CASO 03: En este se tienen dos cordones paralelos y uno ortogonal a ambos:
| a) Vista superior | b) Vista isométrica |
 |
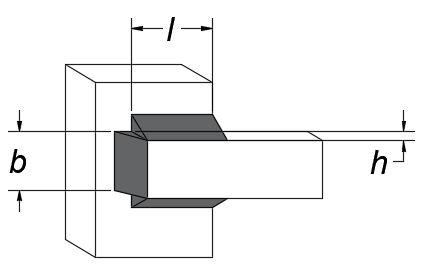 |
Figura 9. Vistas de la soldadura para el caso 03: a) superior, y b) Isométrica Fuente de consulta: autoría propia.
Para este caso, al igual que en los anteriores, se tenía la única diferencia de las longitudes:
![]() (24)
(24)
Con lo cual pudimos desarrollar el esfuerzo, así como los despejes de longitud y fuerza:
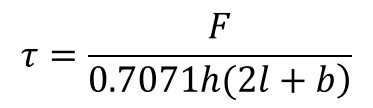 (25)
(25)
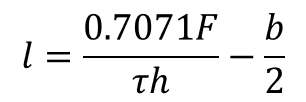 (26)
(26)
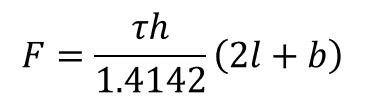 (27)
(27)
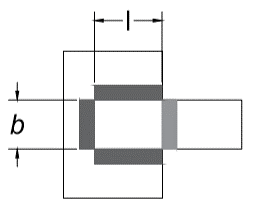
CASO 04: Este es un arreglo cerrado, igualmente cambió la longitud total del arreglo.
| a) Vista superior | b) Vista isométrica |
 |
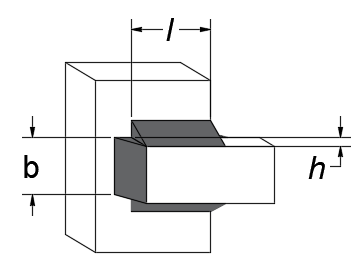 |
Figura 10. Vistas de la soldadura para el caso 04: a) superior, y b) Isométrica Fuente de consulta: autoría propia.
La longitud total del arreglo:
![]() (28)
(28)
El esfuerzo fue igual a:
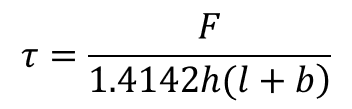 (29)
(29)
Los despejes para la longitud y la fuerza:
![]() (30)
(30)
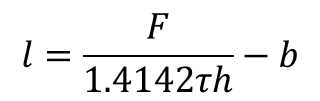 (31)
(31)
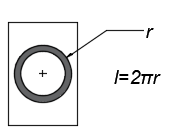
CASO 05: Y, por último, analizamos el caso de un cilindro soldado a una superficie, a lo largo de su periferia.
| a) Vista superior | b) Vista isométrica |
 |
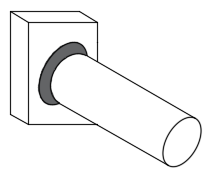 |
Figura 11. Vistas de la soldadura para el caso 05: a) superior, y b) Isométrica Fuente de consulta: autoría propia.
En este caso lo que se hizo fue determinar la longitud del cordón por medio del perímetro, que es una medida bastante aproximada:
![]() (32)
(32)
Determinamos el esfuerzo con base en la ecuación 33:
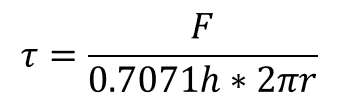 (33)
(33)
Y, como en los anteriores casos, despejamos la longitud (ecuación 34) y la fuerza (ecuación 35):
![]() (34)
(34)
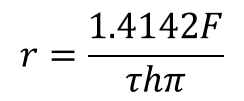 (35)
(35)
Análisis de resultados
Los modelos matemáticos obtenidos para determinar el esfuerzo interno de la soldadura, contienen implícito un margen de error con respecto al esfuerzo al que estarían sometidos en un caso real, esto debido a que la geometría del propio cordón de soldadura es burda, aunado a la existencia de imperfecciones de aplicación que generan pequeños esfuerzos flexionantes debidos a excentricidades6, que tienen un método especifico de cálculo muy diferente a las geometrías de soldadura simétricas sometidas a tracción pura.
También habría que destacar que la resistencia última de cada tipo de soldadura, es, como su nombre lo dice; “última”, es decir que es la máxima fuerza y/o área transversal que puede soportar el arreglo sin llegar una de dos situaciones: la primera si se utiliza una resistencia última de fluencia, antes de que sufra deformaciones permanentes, antes de que empiece a “fluir” el material; y la segunda si se utiliza la resistencia última de tracción, antes de que no soporte más carga la configuración geométrica.
El resultado de la investigación es la redacción de las tablas de este análisis, correspondiente a cada uno de los cinco casos seleccionados.
A continuación, se establece un problema modelo, para tener una idea de la utilización de las tablas de resultados.
Ejemplo:
Se necesita soldar un par de soleras de acero laminado en caliente, en modo de orejas, se requiere soporte de 1,000 kilopondios. La solera tiene las siguientes dimensiones: media pulgada de espesor y cuatro pulgadas de ancho. Si previamente se calculó la resistencia de la solera, y la pared donde irán unidas también es acero laminado (como se ilustra en la Figura 12), seleccione un arreglo soldado, que sea económico y confiable para soportar la carga estática basándose en alguna de las tablas de resultados.
Criterios de diseño:
- Todo lo referente a la resistencia mecánica por parte de la estructura ha sido calculado previamente, dejando como única incógnita la resistencia del material de aporte.
- Para seleccionar el arreglo que mejor se adapte a las necesidades del problema, se considera el que menor material de aporte proporcione; en este caso el primer arreglo.
- Para asegurar su confiabilidad, utilizaremos la formulas correspondientes de las tablas.
Solución:
- Los electrodos más utilizados para aceros bajos en carbono, en este caso acero laminado, son el E60 y E70.
- En esta situación se elige el electrodo E60 porque es más económico.
- Tenemos una placa con un espesor de 1/8 (definido por el problema) y usaremos un electrodo E60, en el apartado correspondiente a los valores anteriores, se multiplica el factor de la tabla por la fuerza que es de 500 kilopondios.
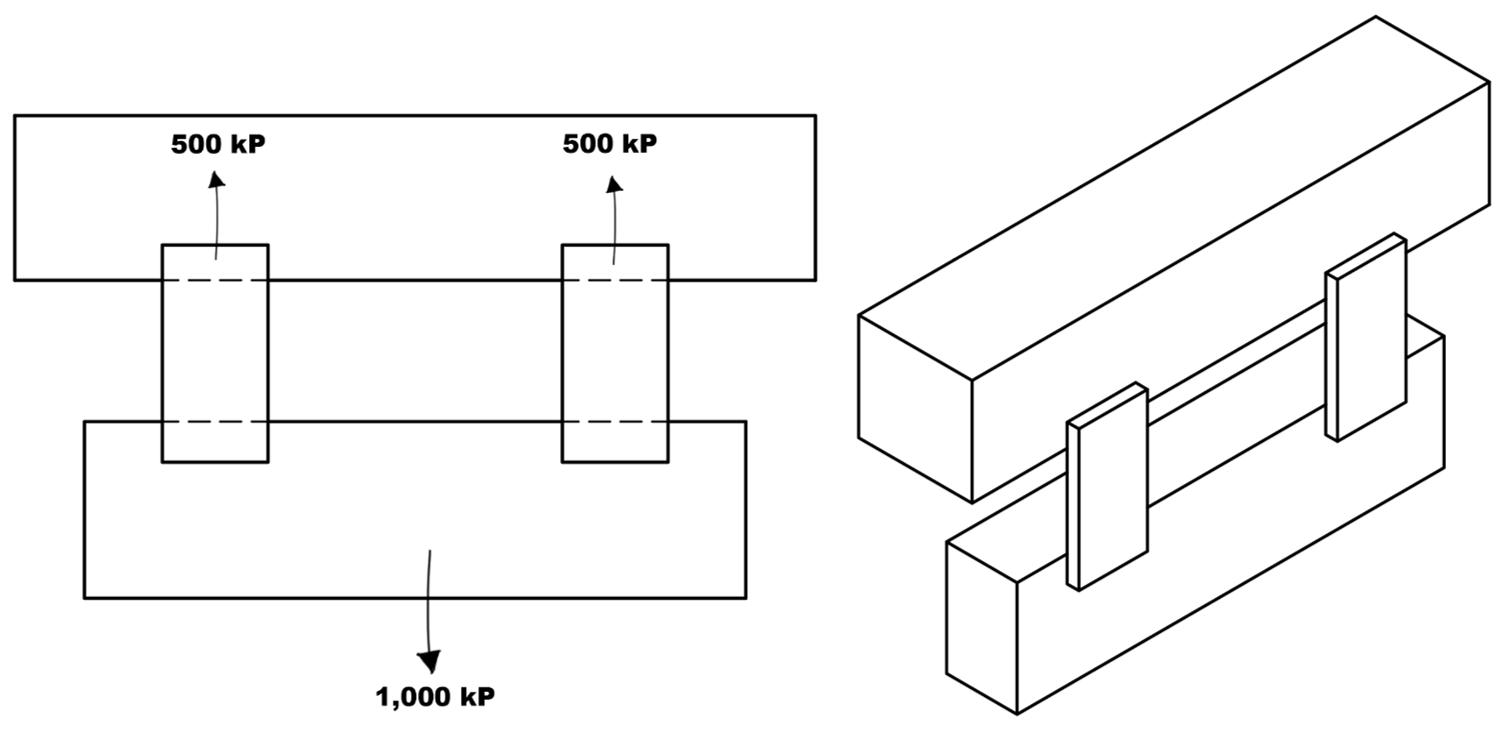
Figura 12. Diagrama de cuerpo libre y vista isométrica Fuente de consulta: autoría propia.
Al consultar la Tabla 01 se observó la siguiente información:

Figura 13. Sección ilustrativa de la Tabla 01, para el ejemplo. Fuente de consulta: Tabla 01.
Seleccionamos la ecuación correspondiente de acuerdo con el Sistema Internacional de Unidades para solera de un octavo:
![]() (36)
(36)
Sustituimos la fuerza resultante en la solera (Figura 12) en la ecuación (36), y obtenemos la longitud mínima para el cordón:
![]() (37)
(37)
Conclusiones del problema:
La longitud resultante (ecuación 37), es una longitud mínima, por lo tanto, se recomienda usar algún factor de seguridad, acorde a la aplicación del arreglo.
Discusión
Como se mencionó en el análisis de resultados, se contempla la resistencia última de tracción y la resistencia última de fluencia, esto quiere decir que no se está incluyendo ningún factor de seguridad, ni por falla estática ni por falla dinámica.
Consideramos que los resultados obtenidos son apropiados para su aplicación en campo, siempre y cuando se interpreten de manera adecuada las tablas y los análisis realizados en la investigación.
Se sugeriría hacer pruebas destructivas para obtener ya sea factores de corrección o factores de seguridad objetivos, con algún criterio de diseño bien fundamentado, basado en métodos numéricos.
Otro aspecto a considerar es que en esta investigación se analizaron arreglos cargados de tal manera que no se generen momentos de inercia, sin embargo, se sugiere hacer un análisis de tales casos, dado que, como ya se mencionó, se generan pequeños esfuerzos flexionantes debido a excentricidades del arreglo.
Conclusiones
La redacción de las tablas para analizar los cinco casos de soldaduras más comunes, facilita la determinación de la fuerza de tracción, fluencia y longitud del cordón de soldadura. Estos resultados dan certidumbre en el uso correcto de la soldadura para que se use de forma eficiente. Las tablas se proporcionan en el siguiente vínculo: https://mega.nz/#!f4szQYAa!wOINEffjrB6-gGA3pc66PUVE0GyHgAt9-E__o44edXE
El realizar este trabajo nos deja como aprendizaje un panorama más amplio en lo que confiere al diseño mecánico, específicamente la soldadura y todas las vertientes que de ella derivan.
Referencias
1. RODRÍGUEZ, Pedro Claudio. Manual de soldadura. 1era. edición. Buenos Aires, Argentina: Librería y editorial Alsina, 2001. p. 5. ISBN: 950-553-095-1
2. MOLERA SOLÁ, Pere. Soldadura industrial: clases y aplicaciones. Barcelona, España: MARCOMBO, S.A., 1992, p. 121.
3. NORRIS, C. H. Photoelastic Investigation of Stress Distribution in Transverse Fillet Welds. Welding J., vol. 24, 1945, p. 557.
4. SALAKIAN, A.G.. Stress Distribution in Fillet Welds: A Review of the Literature. En Welding J., vol. 16, mayo de 1937, pp. 1-24.
5. BEER, Ferdinand P., RUSELL JHONSTON, E. Jr., DEWOLF, Jhon T. y MAZUREK, David T. Mecánica de materiales. Quinta edición. México: Mc Graw Hill, 2010. ISBN: 978-607-15-0263-6.
6. BUDYNAS, Richard G. y NISBETT, J. Keith. Diseño en ingeniería mecánica de Shigley. Novena edición. México: Mc Graw Hill, 2012. ISBN: 1456245236



