Este artículo define los elementos de un control PID y su implementación en Drones para mejorar la estabilización de vuelo y control de maniobras, así como las variables que pueden afectar la eficiencia y desempeño de dispositivos tipo cuadcopter. La implementación se llevó a cabo mediante las librerías de Mega Pirate derivada de Arduo Pilot así como el entorno gráfico de Mission Planner para el control de Drones Multi Rotor, tras la elección de un marco para la implementación (marco forma X) se procedió al control de equilibrio sobre los ejes del Dron.

Palabras Clave: Dron, control, estabilización, PID, equilibrio.

This article defines the elements of a PID control and its implementation in Drones to improve flight stabilizing and control maneuvers, as well as the variables that can affect the efficiency and performance of such cuadcopter devices. The implementation was carried out by bookstores Mega Pirate derivative of Arduo Pilot and graphic environment Mission Planner for control of Drones Multi Rotor, following the election of a framework for implementation (framework form of X) proceeded control balancing on the axles of Dron.

Keywords: Dron, control, stabilization, PID, balance.

La industria de los Drones en la actualidad tiene la atención de diversas áreas de la ingeniería, debido a los usos derivados de esta tecnología algunas ramas de la ingeniería¹ que aportan sus conocimientos son: la electrónica, el aeromodelismo, la programación y la matemática debido a esta gama de áreas involucradas en su desarrollo se tienen avances en su versatilidad así como en las implementaciones de su arquitectura.

Los Cuadcopteros son sistemas de vuelo impulsados por cuatro hélices ubicadas alrededor de un cuerpo principal², la acción dinámica de las fuerzas que actúan sobre el sistema requieren de mecanismos para estabilizarlas y controlar la interacción en un equilibrio constante.

Cada hélice que proporciona un empuje tiene un sentido, un par gira en sentido horario mientras dos giran en sentido anti horario⁹, este movimiento es controlado por sistemas electrónicos denominado ESC (Control de velocidad electrónico).

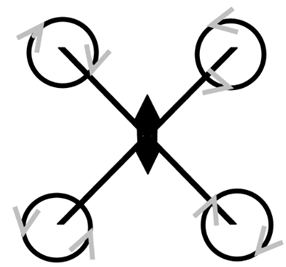
Fig. 1 Movimiento de la hélices frame X. Fuente: Elaboración propia.

La implementación del control PID para el manejo de las fuerzas que actúan sobre el vuelo se han dividido en 3:

1. Control PID Roll o control de giro horizontal el equilibrio del dron se centra en este eje con lo que el control PID es crítico para evitar que el dron gire, a su vez tiene en cuenta que la libertad de maniobra tiene que ser la suficiente como para poder realizar piruetas en 360°.
2. Control PID Yaw o control de giro vertical evita que las fuerzas de movimiento de giro de las hélices hagan que el sistema gire sobre su propio eje, pero deja suficiente libertad para poder orientar la acción de maniobra izquierda y derecha.
3. Control PID pitch o control de elevación mantiene el control de avance o retroceso del sistema dejando la libertad necesaria para acelerar o disminuir la velocidad si las maniobras lo requieren.

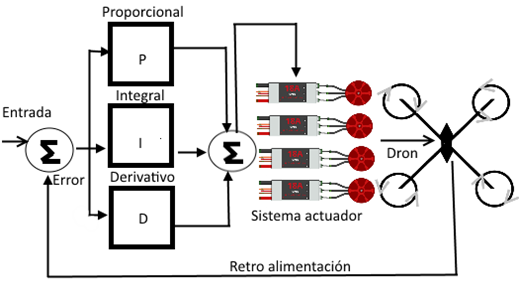
Fig. 2 Diagrama de bloques control PID para Dron. Fuente: Elaboración propia.

El diagrama muestra la interacción de la entrada o señal de los sensores de aceleración y giroscopio del dron con el algoritmo para poder estabilizar los 3 ejes enviando la correcion a los actuadores. Estas señales gracias a las tecnología actual, pueden ser analizadas por micro controladores², que mediante algoritmos analizan las entradas procesando datos y evaluando su corrección con un tiempo de respuesta adecuado. El algoritmo de corrección se basa en la siguiente ecuación:

Donde u(t) es la entrada de control de proceso, e(t) el error de la señal. Kp es la ganancia proporcional, Ti es la constante de tiempo integral, Td la constante de tiempo derivada.

Los motores del tipo Brushles con los que cuenta el dron tiene diferencias significativas con respeto a los motores de corriente continua con escobillas, una de ellas consistente en el rotor, la armadura del motor es la que rota a diferencia de los motores de corriente continua donde el centro es quien gira. La ventaja de esta acción radica en la baja vibración que su diseño proporciona³. La primera fase para crear un sistema estable consiste en tener un actuador estable para posterior mente tratara de aminorar aún más los posibles errores en su desempeño mediante el control PID.

Para poder observar la acción integral, derivativa y proporcional sobre el control de vuelo del dron se montó una estructura metálica en forma de H. Este marco permitirá calcular los efectos de los valores necesarios para mantener el control de una de los tres ejes en el dron. El primero en calcular por tener una relevancia significativa en la estabilización será el Roll⁴ debido a que el proporciona al dron el equilibrio lateral.

El experimento se dividirá en dos partes:

1. Cálculos de los valores necesarios para mantener la estabilidad latera (Roll).
2. Cálculos de los valores necesarios para la estabilidad frontal (Pitch).

Debido a que el control Yaw requiere de un movimiento sobre su propio eje, se propone el cálculo para la implementación PID mediante la relación directa de los datos obtenidos para Pitch y Roll.

1. Cálculo de los valores PID para Roll

El dron se fijó sobre la estructura H con la carga de la batería tal como se haría al tener un vuelo real, la parte frontal se ubicó en el centro de la estructura similar al efecto de balanceo que se tiene en una palanca.

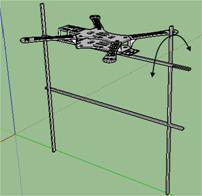
Fig. 3 Cálculo PID de ROLL. Fuente: Elaboración propia.

Los cálculos de las variables de control de errores tienen en cuenta la potencia de los motores es de 980kv ⁵.

rpm = kv * volts
rpm = 980 * 11.1 volts

La cantidad de las revoluciones por minuto que se tiene en un motor de 980 kv como los aplicados en este experimento serían de 10878 rpm.

El valor de las revoluciones que el motor puede alcanzar es relevante para determinar cómo se ajusta la salida a manera de impulsar la entrada hacia el punto de ajuste⁶.

De esta manera se plantea que la señal de control de velocidad tiene que alcanzar un valor de 6.500 como total en el ajuste PID que sería el máximo de revoluciones alcanzadas por el motor. Para obtener este valor en el experimento se tomaron diez lecturas mediante la graficación de los valores arrojados por los sensores del dron.

La siguiente tabla muestra los valores obtenidos en una simulación programada para obtener la estabilización de P o nivel óptimo de señal.

Tabla I Tabla para cálculo de SP simulado

SP	P	P	P
2.000	0.1700	0.0300	0.0700
2.500	0.1700	0.0300	0.0700
3.000	0.1700	0.0300	0.0700
3.500	0.1700	0.0300	0.0700
4.000	0.1700	0.0300	0.0700
4.500	0.1700	0.0300	0.0700
5.000	0.1700	0.0300	0.0700
5.500	0.1700	0.0300	0.0700
6.000	0.1700	0.0300	0.0700
6.500	0.1700	0.0300	0.0700

Fuente: Elaboración propia a partir de datos recabados en interface Mission Planner.

Estos valores con incrementos progresivos fueron obtenidos en el sistema H con el dron ubicado en posición de ajuste del eje roll, se logró obtener un valor estable en la prueba 10 donde el valor de 6.500 mantiene al dron en equilibrio sin fuerzas que interactúen con él.

El control PID tiene que encargarse de equilibrar la horizontal del dron evitando que este gire en el eje Roll. En el caso de los valores P, I, D mediante un simulador programado en C# obtuvimos que el mejor valor asignado para P en un número de interacciones n sería de 0.0500 como lo muestra las siguiente imagen del simulador.

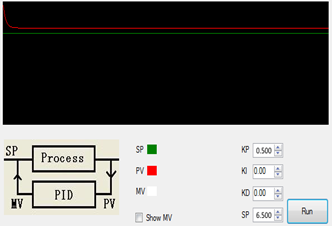
Fig. 4 Simulación de P con un valor estable de 6.500 Fuente: Elaboración propia Interface creada en C# para simulación de PID.

Esta implementación es la ideal por lo que al grabar los parámetros en el sistema de control del dron se obtuvo un sistema lento e inestable por lo que al modificar el valor de P a 0.700 se obtuvo un sistema con mejor ganancia aunque aún inestable por la carencia de los valores I y D del algoritmo de control.

Para calcular a I, el sistema de simulación arrojó el resultado de 0.0430 con este valor la reacción del movimiento para mantener el equilibrio se suaviza evitando un efecto armónico en el control de los errores. El valor de D en simulación arrojó un resultado de 0.150 este parámetro no implica gran mejora pero permite evitar picos de valores de señal en la retro alimentación mejorando con el tiempo la precisión de retorno al valor de estabilización indicado.

Al aplicar los datos obtenidos por simulación en el sistema tipo H se pudo observar que la carga no estaba bien distribuida y debido a esto se tenía un efecto de descompensación por lo que al tratar de mejorar los valores se obtuvieron los siguientes resultados:

SP	P	I	D
6.500	0.0500	0.0430	0.0150
	Reales
SP	P	I	D
6.500	0.0700	0.0500	0.0125

Fuente: Elaboración propia datos ideales simulados y datos reales recabados en dron.

Estos datos se obtuvieron programando la fórmula del control PID en C# el siguiente diagrama muestra la lógica de programación:

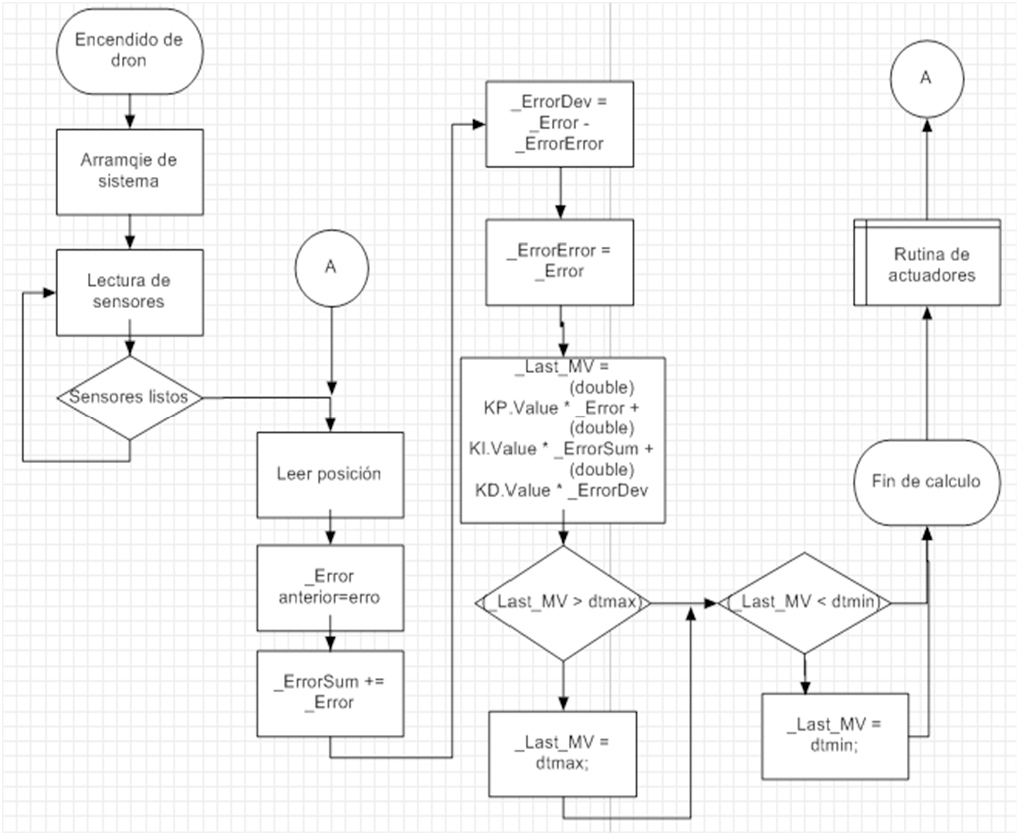
Fig. 5 Simulación de PID en C#. Fuente: Elaboración propia lógica de simulación creada en C#.

Este mismo código se implementó en forma embebida al dron mediante una tarjeta 3M pilot la cual cuenta con un microcontrolador Arduino mega 2560, sensor barométrico, giroscopio, GPS y brújula magnética, de esta forma se tiene un certeza entre la simulación y la acción realizada por el dron. Sin embargo, los valores reales implementados por al dron varían en un porcentaje significativo. Esto debido a cambios en la distribución de la carga así como factores externos de la estructura del dron, pero permiten tener un inicio aproximado para implementar los valores reales⁸.

2. Cálculo de los valores PID para Pitch

El dron se fijó a la estructura H en esta ocasión orientado la parte frontal a un extremo lateral de la barra central y la trasera para hacer el balanceo como lo muestra la siguiente figura.

Figura 5 Cálculo PID de Pitch Fuente: Elaboración propia.

A diferencia del cálculo para la corrección de error del sistema en H en Roll el sistema en H de pitch no requiere de un balanceo constante estable solo requiere de una fuerza constante en dirección frontal o hacia atrás evitando un cambio brusco en el movimiento que aplica al dron.

Los valores de rotación en los motores calculados anteriormente se necesitan para volver aplicar a la ecuación del sistema y teniendo en consideración que previamente se ha balanceado el sistema en el eje Roll los valores a obtener complementan la estabilidad del vuelo del dron.

El valor estable simulado para el eje Pitch arroja un resultado simulado en 4.600 al aplicar el valor en el sistema de control del dron tenemos que es un tanto elevado y brusco el cambio de dirección por lo que se disminuye un 0.1 de la facción obtenida en la simulación quedando con un valor fijo estable de 4.5000 como el valor estable que el sistema deberá de alcanzar.

Los valores obtenidos por simulación en esta ocasión con una corrida de solo seis interacciones de algoritmo PID se muestran en la siguiente tabla:

Tabla para cálculo de SP simulado

SP	P	P	P
2.500	0.0200	0.0250	0.300
3.000	0.0200	0.0250	0.300
3.500	0.0200	0.0250	0.300
4.000	0.0200	0.0250	0.300
4.600	0.0200	0.0250	0.300

Fuente: Elaboración propia datos simulados para estabilidad de dron.

Los valores fueron simulados mediante la lógica del diagrama PID en C#, la siguiente figura muestra la interaccion del simulador y las pruebas reales para la obtención de los valores para P.

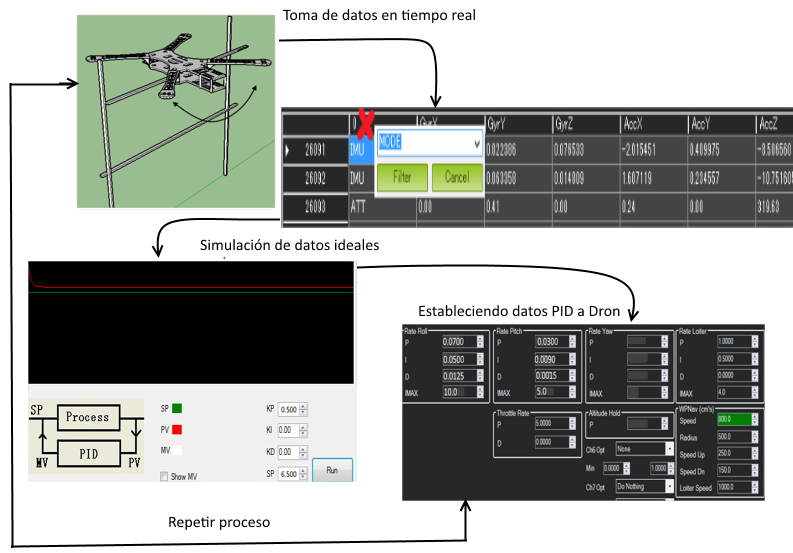
Figura 6. Proceso para cálculo de valores con simulador. Fuente: Elaboración propia proceso de cálculo de variable P.

Basados en el valor real se procedió a simular los valores de ID, el valor de I fue obtenido en 3 interacciones del algoritmo de simulación con un valor ideal de 0.0110 al aplicar los valores al sistema de control se notó que los movimientos eran bruscos en el control del eje Pitch por lo que se decremento en 0.002 obteniendo un valor de 0.0090 con un sistema más estable pero lento en los movimientos. Para el valor de D la simulación arrojo un valor ideal de 0.0015 al aplicar este valor ideal al sistema se observó una reacción estable por lo que no existió la necesidad de modificar el resultado para tener un sistema más estable.

Los valores reales e ideales simulados se muestran en la siguiente tabla:

SP	P	I	D
4.600	0.0300	0.0110	0.0015
	Reales
SP	P	I	D
4.600	0.0300	0.0090	0.0015

Fuente: Elaboración propia datos simulados para variables P,I,D asi como los datos reales para estabilidad de vuelo.

Determinados los valores para dos ejes que permiten la estabilidad horizontal y vertical del dron en el experimento se implementaron los valores mediante la interface gráfica de Mission Planner como se puede observar en la siguiente imagen.

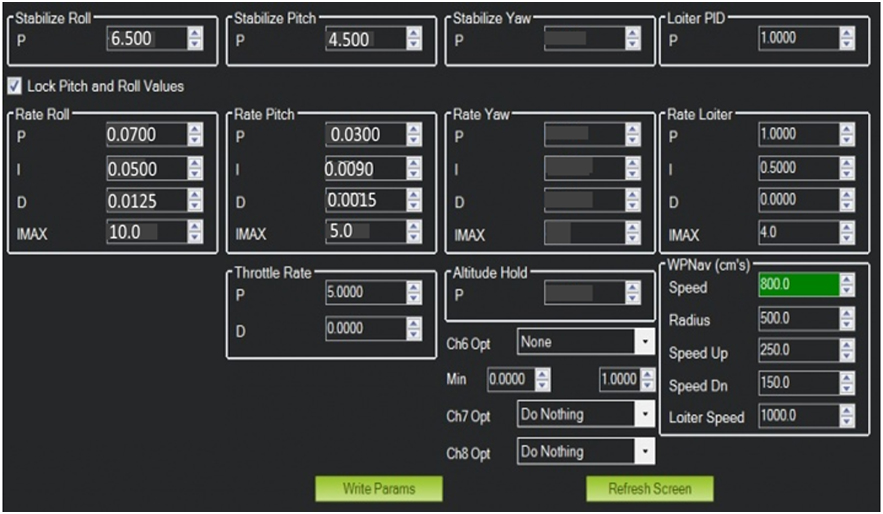
Fig. 7 Parámetros en interface Mission Planner Fuente: Interface Mission Planner configuración de dron.

Usando esta interface para grabar los valores en las variables del sistema, también se pueden leer los valores grabados previamente⁸.

Las herramientas gráficas de Mission Planer permiten observar la acción de los parámetros dentro del sistema del dron y los actuadores¹¹. La siguiente imagen muestra los resultados mediante la herramienta.

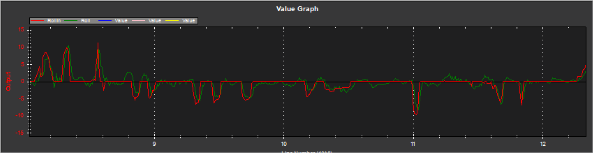
Fig. 8 Datos graficados en Mission Planner tiempo real. Fuente: Interface Mission Planner lectura de sensores.

El software Mission Planner tiene un parámetro extra el cual permite especificar el valor máximo que I puede tener¹⁰ dentro de la ecuación, este parámetro fue calculado por los algoritmos aplicados en la interface llamado auto tuning, también pueden ser calculados modificando la ecuación PID general mediante los métodos como lo son PID por optimización, por parámetro de face o por asignación de polos y cero.

El propósito de este artículo fue definir los cálculos necesarios para las variables del control PID para ser implementadas en el control y estabilización de vuelo en drones, mediante las librerías Mega Pirate en el entorno Mission Planer. Basados en los resultados obtenidos mediante simulación de dos de las tres ejes (Roll y Pitch) podemos concluir que los movimientos en estos son controlados de forma eficiente y con mayor suavidad evitando las inercias provocados por los mismos, con estas variables de control aplicadas a un Cuadcopter se tendrá un vuelo simplificado y mejorado respecto a las órdenes que el sistema recibe vía RF y las compensaciones realizadas debido a variables externas como ráfagas de viento o turbulencia.

En trabajos futuros se pretende comprobar los valores para estabilizar la toma de imágenes mediante cámaras de alta definición así como el posicionamiento y ubicación del dron en un ambiente abierto y cerrado.

1. A. B. L. Y. A. W. Ajanta Ganguly. Design of Tuning method for PID controller using Fuzzy Logic. International Journal of Emerging trends in Engineering and Development. 2013. pp. Volume Issue 3, Vol.5.
2. M. M. H. A. F. M. Atheer L. Salih1. Flight PID controller design for a UAV quadrotor. Scientific Research and Essays Vol. 5(23), pp. 3660-3667, 2010.
3. M. Q. R. G. Dirman Hanafi. Simple GUI Wireless Controller of Quadcopter. In Int. J. Communications. 2013. pp. 52-59 .
4. R. H. B. R. C. Dorf. Modern Control Systems. Addison-Wesley, 1995.
5. D. N. R. C. Edwin Chobot. Design and Implementation of Wireless Sensor and Actuator Network for Energy Measurement and Control at Home. International Journal of Embedded Systems and Applications. 2013. (IJESA) Vol.3, No.1, p. 26.
6. A. Gallaghar. Surveillance UAV. Worchester Polytechnic Institute. 2014. pp. 75-80.
7. T. Jirinec. Stabilization and control of unmanned quadcopter. Master’s thesis, CZECH TECHNICAL UNIVERSITY IN PRAGUE. 2011. p. 45.
8. M. Kurien. Overview of different approach of PID controller tuning. International Journal of Research in Advent Technology. 2011. pp. E-ISSN: 2321–9637.
9. K. Ogata. Modern Control Engineering. Prentice Hall - Br, 1999.
10. M. W. S. S. Vitul Varshney. PID based Stabilization of Gesture Controlled. International Journal of Engineering and Advanced Technology (IJEAT). 2014. pp. ISSN: 2249 – 8958, Volume-3 Issue-6.
11. D. Vrančić. A New PID Controller Auto-tuning Method based on Multiple Integrations. J. Stefan Institute. 2012. p. 39.