Año 8, Número 1. Septiembre - Diciembre, 2020. 
Diseño de un calentador híbrido solar/inducción optimizado mediante inteligencia artificial
Design of a hybrid solar / induction heater optimized by artificial intelligence
Instituto Tecnológico Superior de Purísima del Rincón
Por: Valentín Calzada Ledesma, Juan de Anda Suárez, Sergio Rodríguez Miranda y Pedro M. Cuevas González / Ver en pantalla completa
Resumen
Un calentador de agua es un dispositivo termodinámico que utiliza diferentes fuentes de energía, entre ellas destacan la electricidad, los combustibles y la energía solar. Sin embargo, bajo ciertas condiciones, estas tecnologías desprenden ventajas y desventajas. En este artículo se propone el diseño de un calentador híbrido, con el cual se busca aprovechar en mayor medida la energía solar y como sistema de respaldo, ante adversidades climáticas, tecnología de inducción magnética. El diseño está optimizado para maximizar la temperatura del agua y a su vez minimizar la cantidad de energía eléctrica consumida, mejorando la eficiencia del calentador. Para lograrlo, se emplean diferentes herramientas, como la simulación, la física computacional y la inteligencia artificial.
Palabras clave: física computacional, termodinámica, calentador solar, inducción magnética.
Abstract
A water heater is a thermodynamic device that uses different sources of energy, among them solar energy, fuels, and electricity. However, under certain conditions, these technologies present advantages and disadvantages. In this article, the design of a hybrid-heater is proposed, with which it is intended to make the most of solar energy and in the event of climatic adversities, magnetic induction technology as a backup system. The hybrid design is optimized to minimize the amount of electrical energy consumed and at the same time maximize the water temperature, in this way improving the efficiency of the heater. To achieve this, different tools are used, such as computational physics, and artificial intelligence.
Keywords: computational physics, thermo-dynamics, solar heater, magnetic induction.
Introducción
Un calentador de agua es un dispositivo termodinámico que utiliza energía para incrementar la temperatura del agua. Entre las diferentes fuentes de energía destacan: la electricidad, los combustibles (principalmente gas y derivados del petróleo) y la energía solar, las cuales han sido implementadas con éxito en la industria. Sin embargo, bajo ciertas condiciones, de estas tecnologías se desprenden ventajas y desventajas. Por ejemplo, los calentadores que utilizan energía solar pueden lograr una eficiencia del 94 al 96 % durante la transferencia de la energía solar1, manteniendo la temperatura del agua entre los 65 y 105 °C en un día soleado; sin embargo, cuando las condiciones climáticas no son adecuadas (por ejemplo, nieve, días nublados o lluvia), esa eficiencia cae drásticamente.
Por otro lado, se encuentran los calentadores que utilizan combustibles como el gas natural o hidrocarburos2. A pesar de que este tipo de dispositivos son comúnmente utilizados en hogares y para procesos industriales, su uso cotidiano a largo plazo no es favorable para el medio ambiente, debido a las altas emisiones de gas contaminante. Además, el alza de precios de los combustibles, los convierte en sistemas poco redituables (Sahnoune, Madani, Zelmat & Belhamela, 2014)3.
Respecto a los sistemas que utilizan energía eléctrica, en la industria se pueden encontrar dos tipos de calentadores: los de resistencia y los de inducción magnética. Este tipo de dispositivos son capaces de calentar el agua a una temperatura de 35 °C en un tiempo aproximado de tres minutos, logrando una eficiencia de transferencia de energía del 98 al 99 % (Hohne, Kusakana y Numbi, 2019)4; sin embargo, los dispositivos de resistencia tienen un consumo de potencia eléctrica elevado, aproximadamente de 1 a 1.5 KW/h, cantidad que es penalizada en algunos países, por lo que su uso cotidiano no es favorable (Balke, Healy y Ullah, 2016)5. Por otro lado, en el estado del arte se ha reportado que los dispositivos de inducción magnética consumen menos potencia eléctrica, por lo tanto, el diseño de dispositivos de calentamiento por inducción es favorable para el ahorro de energía eléctrica6.
Con base en lo mencionado previamente, una alternativa para solucionar el problema del calentamiento de agua es diseñar sistemas híbridos que implementen tecnologías eficientes y amigables con el medio ambiente. Por lo que en este artículo se propone el diseño de un sistema de este tipo, con el cual se busca aprovechar en mayor medida la energía solar y, como sistema de respaldo (ante adversidades climáticas), tecnología de inducción electromagnética.
Existen trabajos similares en el estado del arte, en donde se exploran diversos algoritmos para realizar el diseño de sistemas eléctricos (Masuda, Okamoto, & Wakao, 2019; Naar & Bay, 2013)7, 8, sin embargo, hay menos trabajos en donde se implementen para el diseño termodinámico de un calentador solar (Sadeghi, 2020; Colacurcio, 2019; Ahmadi, 2013)9, 10, 11.
Planteamiento del problema
Diseñar un calentador de agua bajo un enfoque híbrido es un reto, ya que hay diversos factores a considerar; sin embargo, se puntualizan dos problemas sustanciales con los que se deben lidiar:
- Para diseñar un inductor electromagnético, es necesario definir el tipo y el tamaño de la bobina, así como el solenoide.
- En cuanto al sistema completo, es de suma importancia definir cuál es el volumen óptimo de calentamiento de agua, para minimizar el consumo de corriente eléctrica.
Para dar solución a estos problemas se debe modelar la física que impera en el proceso de transferencia de calor, tanto de manera solar como inductiva. A su vez, se debe optimizar la interacción entre ambos enfoques, lo cual es una tarea de suma dificultad, ya que se involucra un conocimiento multidisciplinario.
Objetivo
Realizar el diseño de un calentador híbrido mediante el uso de inteligencia artificial, empleando un algoritmo de optimización computacional llamado SEED (detallado en la sección Estimación de Distribución basada en Energía de aproximación Simétrica).
A grandes rasgos, se propone un esquema que proporciona una serie de soluciones candidatas al problema, cuya eficiencia es medida a través de una función de costo (detallada en la sección de Metodología), la cual modela la interacción entre la tecnología solar e inductiva. Los valores obtenidos por la función de costo para cada una de las soluciones candidatas, retroalimentan a la inteligencia artificial, permitiéndole generar cada vez mejores soluciones para resolver el problema.
A continuación, se muestran una serie de conceptos para comprender detalladamente la propuesta.
Marco teórico
En la Figura 1, se muestra el esquema general del sistema híbrido (solar/inducción) de calentamiento de agua propuesto en este artículo.
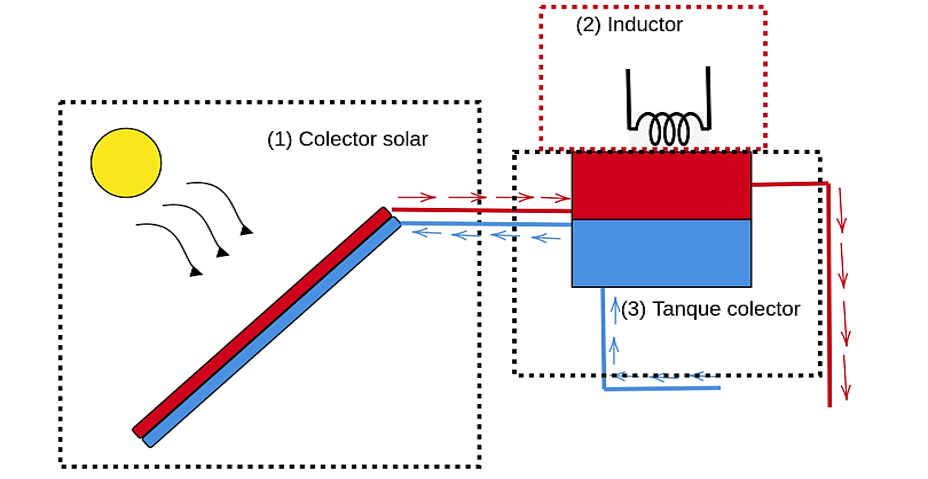
Figura 1. Esquema general del sistema calentador solar e inductor. Fuente: elaboración propia.
Comenzando con el colector solar, la potencia de emisión de energía calorífica proveniente del Sol puede ser estimada por la ley de Stefan-Boltzmann, dada por la Ec. 1.
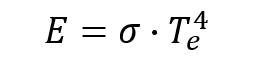 (1)
(1)
donde E es la potencia de emisión dada por las unidades ,
es la constante de Stefan-Boltzmann con valor de
y
es la temperatura efectiva. Si se multiplica la Ec. 1 por la superficie de emisión del Sol, dada por
, se obtiene una potencia solar de
, la potencia mencionada anteriormente debe ser aprovechada en cierta proporción dependiendo de la geometría del colector solar en la Figura 1, esto se profundiza en la siguiente sección.
Principio termodinámico del calentador solar
Para modelar el comportamiento del termo-fluido, en este caso agua, la primera aproximación se comporta como un fluido incompresible y no viscoso, lo que se puede describir mediante las ecuaciones de Navier-Stokes para la conservación de la energía (Ec. 2).
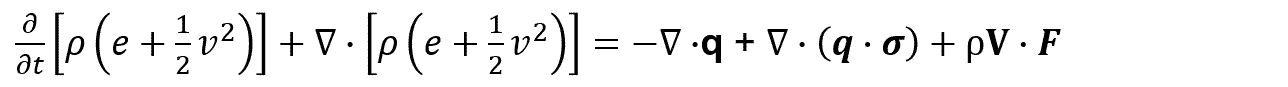 (2)
(2)
donde es la densidad del fluido,
la energía interna, V es la velocidad, F es la fuerza, y q es la cantidad de energía calorífica. En el estándar de producción y diseño de colectores de energía térmica solar, se emplea la geometría cilíndrica, de manera que la Ec. 2 es transformada a simetría cilíndrica por simplicidad de solución numérica, y considerando a la Ec. 2 en términos de la temperatura del sistema, esta se transforma en la Ec. 3 (Wannagosit C. S.-l., 2018)11.
donde es la difusividad térmica,
el flujo de energía calorífica y k la conductividad térmica. La Ec. 2 como ya se mencionó, representa la ecuación fundamental de energía en el fluido, sin embargo, el sistema térmico completo de un calentador solar, en general está caracterizado por un termosifón y un colector de trasmisión, estos se describen detalladamente en las secciones siguientes.
Termosifón
El efecto termosifón es un fenómeno físico que se produce en los fluidos cuando se calientan. Usualmente se presentan dos estados termodinámicos, los cuales son:
- El agua fría es conducida mediante la fuerza de gravedad desde el tanque contenedor hacia la parte inferior de los tubos de calentamiento, como se muestra en la Figura 2. Debido a la radiación solar, el agua es calentada y empujada por el choque térmico a la parte superior del tanque.
- Dado que el agua caliente es menos densa que el agua fría, esta se mantiene siempre en la parte superior (ver Figura 2), generando choques térmicos del fluido, manteniendo un ciclo giratorio en el sistema que distribuye el agua caliente.
En términos matemáticos, un termosifón se puede modelar utilizando la Ec. 3, esta se puede dividir en tres secciones principales: la evaporación, la adiabática y la condensación, la cuales son modeladas por las Ecs. 4, 5 y 6.
Discretizando la Ec. 3 en términos de diferencias finitas, se tiene que la temperatura de evaporación del fluido (Ec. 4) es simbolizada a la derecha por y
a la izquierda. Para la región de condensación, el modelo está dado por la Ec. 5.
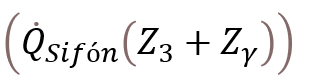 (5)
(5)
donde y
son conocidas como resistencias térmicas y
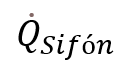 el remanente de energía térmica. Finalmente, la Ec. 6 describe la ecuación fundamental del termosifón.
el remanente de energía térmica. Finalmente, la Ec. 6 describe la ecuación fundamental del termosifón.
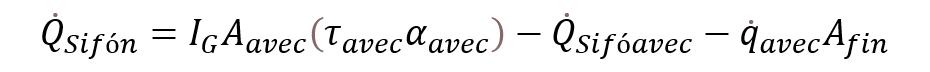 (6)
(6)
donde 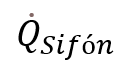 representa la energía calorífica en el sistema de sifón, y
representa la energía calorífica en el sistema de sifón, y son parámetros de absorción superficial (Wannagosit, Sakulchangsatjatai, Kammuang-lue, & Terdtoon, 2018)12.
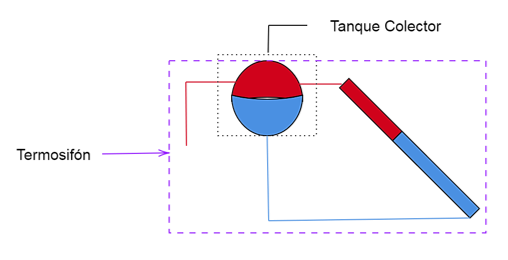
Figura 2. Esquema general del termosifón. Fuente: elaboración propia.
Calentamiento por inducción electromagnética
De manera general, estos sistemas generan un campo magnético mediante la circulación de una corriente eléctrica en una bobina, produciendo calor debido la resistencia de dicha corriente, a este fenómeno se le conoce como el efecto Joule. Para modelar el calentamiento por inducción electromagnética, se emplea la ecuación de Ampere en su estado casi estático, lo que elimina el desplazamiento de la corriente eléctrica, esto describe en la Ec. 7.
Por otro lado, tomando la ecuación de Faraday, dividiéndola por la ecuación del campo magnético y aplicándole el operador rotacional, se obtiene la Ec. 8.
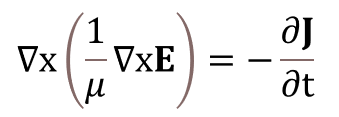 (8)
(8)
Finalmente, la Ec. 9 describe de manera total el cambio parcial de campo eléctrico en el tiempo, con respecto al cambio parcial de la corriente en el tiempo (Bay, Labbe, Favennec, & Chenot, 2003)13, mejor conocida como la ecuación general para la inducción electromagnética.
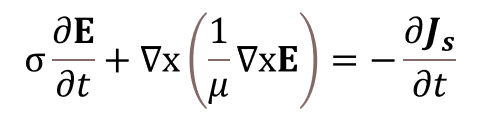 (9)
(9)
Para realizar la simulación del calentador solar, las Ecs. 2 - 9 se implementaron en COMSOL Multiphysics, el cual es un software empleado para el análisis y resolución de problemas de la física e ingeniería mediante elemento finito. En la siguiente sección se detalla el funcionamiento de los algoritmos para la optimización de los parámetros de los modelos electro-térmicos, los cuales a su vez se comunican con COMSOL Multiphysics para optimizar la simulación.
Optimización computacional
La optimización computacional se refiere a un conjunto de métodos que buscan dar solución a un problema modelado matemáticamente, el cual se desea optimizar, es decir, encontrar su punto mínimo o máximo. Un tipo particular de métodos de optimización computacional son las metaheurísticas, las cuales implementan estrategias que guían a un conjunto de soluciones candidatas (generadas aleatoriamente) hacia un óptimo, en el mejor de los casos el óptimo global de una función de costo, también llamada función objetivo, cuyas variables o parámetros a optimizar se encuentran acorde al domino del problema.
Un tipo particular de metaheurísticas son los Algoritmos de Estimación de Distribución (EDAs por sus siglas en inglés). Las EDAs construyen modelos probabilísticos explícitos que se refinan de forma iterativa para producir soluciones cada vez mejores para un problema particular. Esta característica permite a las EDAs la capacidad de adaptarse a la estructura del problema a optimizar, logrando reducir su costo computacional.
Una de las EDAs que ha mostrado una mayor eficiencia ante problemas de dominio continuo es el algoritmo de Estimación de Distribución basada en Energía de aproximación Simétrica (SEED, por sus siglas en inglés). Este algoritmo es el seleccionado para optimizar el problema planteado esta investigación, debido a que no se requieren parámetros externos para su funcionamiento, solo la población inicial. Además, el algoritmo SEED es capaz de encontrar soluciones de manera rápida, reduciendo así el costo computacional necesario. A continuación, se detalla de manera puntual su funcionamiento (De Anda-Suárez & Calzada-Ledesma, 2019)14.
Estimación de Distribución basada en Energía de aproximación Simétrica (SEED)
En años recientes, los científicos han tornado su atención hacia la función de distribución de probabilidad de Boltzmann (Ec. 10), ya que proporciona diversas ventajas cuando esta se implementa en EDAs basadas en energía.
Sin embargo, diversos estudios en el estado del arte reportan que el muestreo directo de la función Boltzmann, para actualizar el modelo probabilístico, no es práctico. Para resolver esto, SEED emplea una aproximación a la función Boltzmann mediante una distribución gaussiana con parámetros (Ec. 11) y
(Ec. 12), esto a través de la minimización de la divergencia Jeffreys calculada entre las funciones gaussiana
y Boltzmann
, con el fin de utilizar esa distribución como modelo probabilístico.
,
(11)
 (12)
(12)
A diferencia de otras EDAs basadas en Boltzmann, en donde el parámetro de Boltzmann se determina de manera heurística, SEED se caracteriza por calcular este valor de manera autoadaptativa al problema (De Anda-Suárez & Calzada-Ledesma, 2019)14.
Algoritmo SEED
Al inicio del algoritmo, una población de N soluciones se inicializa bajo una distribución uniforme y se evalúa utilizando una función objetivo. Se denota un individuo de la población como
y
para
, los valores objetivo. Después de que la población es evaluada, con el fin de reducir el costo computacional, esta se ordena en función de
, en donde el primer elemento de la población es el mejor individuo, denotado como
.
Posteriormente, una muestra de la población ordenada es seleccionada por medio de un truncamiento, y con esta se construye el modelo probabilístico.
Después una nueva población es muestreada a partir de una distribución normal con parámetros
y >
(2 y 3 respectivamente para cada dimensión del vector).
Al final, si ,
se incorpora en la nueva población. El algoritmo SEED continúa en el ciclo de convergencia hasta cumplir con un criterio de paro, usualmente un número definido de t iteraciones o hasta alcanzar el valor objetivo deseado (De Anda-Suárez & Calzada-Ledesma, 2019)14.
Diseño optimizado mediante algoritmos evolutivos
El proceso evolutivo tiene como objetivo encontrar los parámetros adecuados para el diseño del tubo de calentamiento, la geometría del tanque colector y por último el diseño del inductor. En la Figura 3, se muestra el diagrama general de la metodología para el proceso de optimización de parámetros.
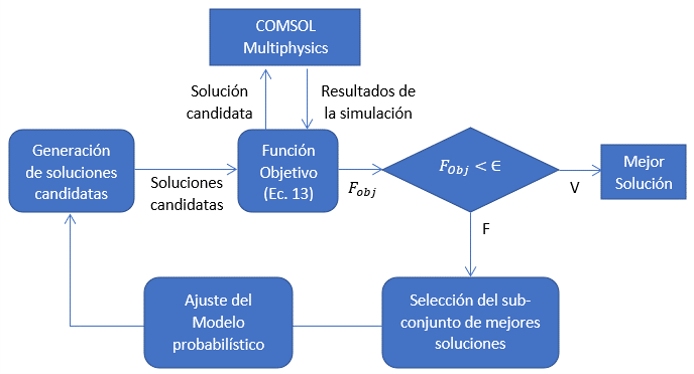
Figura 3. Optimización de parámetros mediante SEED. Fuente: elaboración propia.
Metodología
A continuación, se muestra una descripción detallada del proceso de optimización ilustrado en la Figura 3.
1.- Se establecen los parámetros electro-térmicos a optimizar para el diseño del calentador solar y el inductor electromagnético, estos se muestran a continuación:
- Se establecen los parámetros electro-térmicos a optimizar para el diseño del calentador solar y el inductor electromagnético, estos se muestran a continuación:
Tabla 1. Parámetros para calentador solar. Fuente: elaboración propia.
| Parámetro | Descripción | Dominio |
| L | Longitud del tubo | De 0.5 a 1.5 m |
| D | Diámetro del tubo | De 0.05 a 0.1 m |
| V | Volumen del contenedor | De 10 a 50 L |
Tabla 2. Parámetros para inductor electromagnético. Fuente: elaboración propia.
| Parámetros | Descripción | Dominio |
| N | Número de vueltas de la bobina por capa | De 10 a 500 |
| L | Longitud del tubo de transfería de calor | De 0.1 a 0.2 m |
| F | Frecuencia de oscilación | De 70 kHz a 100 kHz |
2.- Para esta experimentación, el algoritmo SEED se configura con una población inicial de 50 soluciones candidatas de dimensión 6 (el total de parámetros), es decir, una población de configuraciones de parámetros “aleatorios”, cuya eficiencia se medirá con la función objetivo (Ec. 13), la cual está diseñada para maximizar la temperatura del agua y a su vez minimizar la cantidad de energía eléctrica consumida.
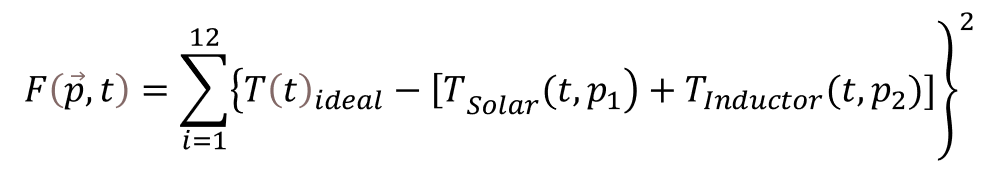 (13)
(13)
donde es la temperatura ideal para el consumo humano, según el cambio de estaciones en el año,
es la temperatura alcanzada por la simulación de COMSOL, mientras que
es el resultado de la simulación del sistema inductor. Por último,
y
son el conjunto de parámetros de simulación para el calentador y el inductor respectivamente, descritos en las Tablas 1 y 2.
3.- El cálculo de la función objetivo depende de los resultados obtenidos por las simulaciones en COMSOL Multiphysics, por lo tanto, una vez medida la eficiencia de cada una de las soluciones candidatas de la población en curso, la información obtenida se retroalimentará al algoritmo SEED, permitiéndole ajustar o evolucionar el modelo probabilístico (véase la sección de Estimación de Distribución basada en Energía de aproximación Simétrica —SEED—) para generar una nueva población de soluciones, las cuales se evaluarán nuevamente con la función objetivo.
4.- El proceso evolutivo se realiza de manera iterativa hasta encontrar la mejor configuración de parámetros que optimice la función objetivo.
5.- Como se mencionó en la sección titulada Algoritmo SEED, se debe establecer un criterio de paro, para este caso particular, el proceso evolutivo se detendrá si alguna de las soluciones candidatas llega a un valor objetivo menor a un margen de error
o si se cumplen un total de 50,000 iteraciones.
6.- La experimentación se realizó en una computadora con Linux OS, procesador i7 y 16 GB de memoria RAM. La implementación de SEED se realizó en el lenguaje de programación Python. El cual se encuentra disponible en la siguiente liga: https://github.com/LIDT-Lab/pySEED
Cabe señalar que las simulaciones gráficas en COMSOL Multiphysics, para todas las soluciones candidatas, no se realizaron durante el proceso evolutivo, ya que esto supondría un costo computacional considerable. En este sentido, para fines ilustrativos, se simula gráficamente el modelo de acoplamiento entre el calentador solar y el inductor electromagnético, con la mejor configuración de parámetros encontrada por SEED, la cual está calibrada para maximizar la temperatura del agua, minimizando la cantidad de energía eléctrica consumida.
Resultados
En la presente sección, se muestra la simulación gráfica (Figura 4) realizada con los parámetros reportados en las Tablas 3 y 4.
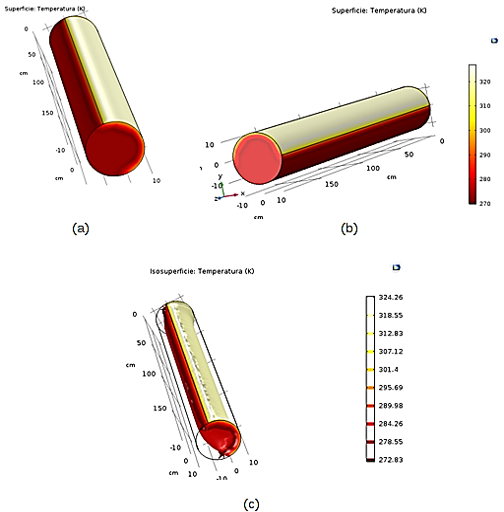
Figura 4. Simulación gráfica del tubo de calentamiento por transferencia de energía solar. Fuente: elaboración propia.
En la Tabla 3 se muestran los valores óptimos de los parámetros, encontrados mediante SEED, para diseñar la geometría del contenedor del calentador solar.
Tabla 3. Parámetros óptimos para la geometría del contenedor. Fuente: elaboración propia.
| Parámetro | Descripción | Dominio |
| L | Longitud del contenedor | 1.5 m |
| D | Diámetro del contenedor | 17 cm |
| V | Volumen del contenedor | 25 L |
En la Tabla 4 se muestran los valores óptimos de los parámetros encontrados por SEED, para diseñar el inductor electromagnético.
Tabla 4. Parámetros óptimos para el diseño del inductor. Fuente: elaboración propia.
| Parámetros | Descripción | Dominio |
| N | Número de vueltas de la bobina | 125 |
| L | Longitud del tubo de transfería de calor | 12 cm |
| F | Frecuencia de oscilación | 75 KHz |
Discusión de resultados
En las Figuras 4a y 4b se muestra la simulación gráfica del tubo de calentamiento, el cual absorbe la energía calorífica proveniente del Sol. La región más clara, representa la zona más caliente en el tubo, cuya temperatura es superior a los 320 °K (aproximadamente 47 °C), adecuada para el consumo humano. Por otro lado, la región más oscura representa la zona más fría, en la simulación se consideran temperaturas debajo de los 0 °C; sin embargo, en la práctica, la temperatura de esta zona estará acotada a la temperatura ambiente. Finalmente, en la Figura 4c, se muestra el resultado de las zonas de transferencia de energía calorífica del sistema.
En los resultados mostrados en la Tabla 3 se puede observar que, debido a la implementación del inductor electromagnético en el sistema de calentamiento, se redujeron las dimensiones del contenedor, lo que permite crear sistemas eficientes a un menor costo, ya que los contenedores existentes en el mercado son de 1.8 m de longitud y 25 cm de diámetro. El volumen del contenedor diseñado por el algoritmo SEED es de 25 L, el cual es adecuado para el uso humano. Cabe señalarse que, en la práctica, se deben añadir paredes adiabáticas para minimizar la pérdida de energía calorífica y se debe tener en cuenta que esto incrementa ligeramente las dimensiones del contenedor.
Finalmente, en la Tabla 4 se puede observar que el número de vueltas por capa del inductor es de 125, esto es importante, ya que el alambre de cobre necesario para crear el inductor es relativamente poco, comparado con los inductores estándar, lo cual permite una reducción de costos para su fabricación. La longitud del tubo de transferencia de calor es de 12 cm. Finalmente, la frecuencia de oscilación es de 75 KHz, lo que permite ajustarse a los elementos electrónicos en el mercado.
Conclusiones
Con base en la experimentación realizada, se concluye que es posible realizar el diseño optimizado de un calentador híbrido solar/inducción, obteniendo resultados que permiten a futuro la manufacturación real de dicho sistema a un bajo costo, esto debido a la optimización realizada por el algoritmo SEED.
Un aporte esencial es el acoplamiento del algoritmo SEED a la simulación física de COMSOL, a través de la función objetivo diseñada. Por lo que hemos investigado en el estado del arte, este tipo de enfoques son pocos, por lo cual consideramos que estas aplicaciones pueden ser ampliamente explotadas en el campo de la física computacional para el diseño de sistemas termodinámicos.
Como trabajo futuro, pretendemos realizar la manufactura real del diseño aquí presentado, añadiendo un sistema basado en inteligencia artificial e Internet de las cosas, para monitorear y predecir el cambio climático, de manera que se pueda implementar un sistema de orientación solar, proporcionando una mejor experiencia al usuario(a).
Referencias
1. SUBRAMANI, J. et al. Efficiency and heat transfer improvements in a parabolic trough solar collector using TiO2 nanofluids under turbulent flow regime. Renewable energy, 2018,119: 19-31. ISSN: 0960-1481
2. HAINES, Victoria; KYRIAKOPOULOU, Konstantina; LAWTON, Clare. End user engagement with domestic hot water heating systems: Design implications for future thermal storage technologies. Energy Research & Social Science, 2019, 49: 74-81. ISSN: 2214-6296
3. SAHNOUNE, F., et al. Comparative study between solar and conventional heating–economic study and environmental impact. Energy Procedia, 2014, 50: 841-852. ISSN: 1876-6102
4. HOHNE, P. A.; KUSAKANA, K.; NUMBI, B. P. A review of water heating technologies: An application to the South African context. Energy Reports, 2019, 5: 1-19. ISSN: 2352-4847
5. BALKE, Elizabeth C.; HEALY, William M.; ULLAH, Tania. An assessment of efficient water heating options for an all-electric single family residence in a mixed-humid climate. Energy and buildings, 2016,133: 371-380. ISSN: 0378-7788
6. JORDAN, A., et al. Inductive heating of ferrimagnetic particles and magnetic fluids: physical evaluation of their potential for hyperthermia. International Journal of Hyperthermia, 1993, 9 (1): 51-68. ISSN: 1464-5157
7. MASUDA, Hiroshi; OKAMOTO, Yoshifumi; WAKAO, Shinji. Multistage topology optimization of induction heating apparatus in time domain electromagnetic field with magnetic nonlinearity. COMPEL-The international journal for computation and mathematics in electrical and electronic engineering, 2019. ISSN: 0332-1649
8. NAAR, Raphaëlle; BAY, François. Numerical optimisation for induction heat treatment processes. Applied Mathematical Modelling, 2013, 37 (4): 2074-2085. ISSN: 0307-904X
9. SADEGHI, Gholamabbas; NAJAFZADEH, Mohammad; AMERI, Mehran. Thermal characteristics of evacuated tube solar collectors with coil inside: An experimental study and evolutionary algorithms. Renewable Energy, 2020, 151: 575-588. ISSN: 0960-1481
10. COLACURCIO, Giovanni, et al. Multiobjective household energy planning using evolutionary algorithms. En Ibero-American Congress on Information Management and Big Data. Springer, Cham, 2019: 269-284.
11. AHMADI, Pouria; DINCER, Ibrahim; ROSEN, Marc A. Thermodynamic modeling and multi-objective evolutionary-based optimization of a new multigeneration energy system. Energy Conversion and Management, 2013, 76: 282-300. ISSN: 0196-8904
12. WANNAGOSIT, C., et al. Validated mathematical models of a solar water heater system with thermosyphon evacuated tube collectors. Case studies in thermal engineering, 2018,12: 528-536. ISSN: 2214-157X
13. BAY, François, et al. A numerical model for induction heating processes coupling electromagnetism and thermomechanics. International journal for numerical methods in engineering, 2003,58 (6): 839-867. ISSN:1097-0207
14. DE ANDA-SUÁREZ, Juan; CALZADA-LEDESMA, Valentín, et al. Symmetric-Approximation Energy-Based Estimation of Distribution (SEED): A Continuous Optimization Algorithm. IEEE Access, 2019, 7: 154859-154871.



