En este artículo se presenta la implementación de la técnica óptica de Deflexión de Franjas (FD), la cual emplea el principio de deflexión de rayos, para el análisis en la variación de temperaturas para una distribución del índice de refracción gaussiana en un medio de propagación transparente. El principio de este método es la comparación entre la imagen deformada y la imagen de referencia de un fondo establecido, utilizando el método de Fourier para recuperar la fase. Los resultados permiten conocer el proceso de combustión, además de la implementación, bajo costo y amplias posibilidades de aplicación de la técnica en ambientes industriales donde existen gradientes de temperatura altos (entre 700 y 1600 °C). Así pues, una posible aplicación de los resultados de este estudio es utilizarlos como base para estudios de transferencia de calor en aparatos eléctricos.

Palabras clave: deflexión de rayos, temperatura, deflexión de franjas.

This research work presents the implementation of the optical technique of Deflection of Fringes (FD), which uses the principle of deflection of rays, for the analysis in the temperature variation for a distribution of the Gaussian refractive index in a medium of propagation transparent. The principle of this method is the comparison between the distorted image and the reference image of an established background, using the Fourier method to recover the phase. The results provide insight into the combustion process, in addition to the implementation, low cost and wide possibilities of application of the technique in industrial environments where there are high temperature gradients (between 700 and 1600 ° C). Thus, a possible application of the results of this study is to use them as a basis for studies of heat transfer in electrical appliances.

Keywords: rays deflexion , temperature, fringes deflexion.

El ser humano se ha dado cuenta de la importancia de medir. Medir es aprender, es ampliar los sentidos sensoriales, y con esto, tener más información que ayude a entender mejor y tomar decisiones más acertadas en la transformación y convivencia con la naturaleza. Después de todo, ¿a quién no le gustaría poder tener el control sobre cada situación vivida o conocer las consecuencias sobre cada una de ellas?

Es por esto que ha existido desde el comienzo de la humanidad el interés por estudiar y desarrollar instrumentos y técnicas de medición en los distintos campos de la ciencia y la tecnología. Técnicas de medición que permitan interrogar, caracterizar y visualizar un amplio espectro de fenómenos físicos.

La combustión, uno de estos fenómenos, ocurre debido a complejas interacciones entre reacciones químicas y transferencias de calor, masa y momento. La temperatura es consecuencia clave de estas interacciones, por lo cual es de vital importancia medirla, y en los tiempos actuales cada vez con mayor precisión, lo que permite conocer más a fondo el proceso de combustión y esto a su vez ayuda a optimizar recursos, en este caso energéticos, un problema muy vigente en la actualidad.

El empleo de técnicas ópticas para la “medición” de parámetros físicos tales como temperatura^1-5, velocidad⁶ y flujo de masas⁷, presenta ventajas con respecto al uso de dispositivos mecánicos, por ser de carácter no intrusivo, puesto que no insertan una perturbación en el flujo natural del fenómeno analizado, lo que sí ocurre en la medición directa. La mayoría de los métodos ópticos usados para analizar la combustión fueron descubiertos hace 30 años, sin embargo, debido al reciente desarrollo de fuentes de luz, sensores y técnicas computacionales para la evaluación de mediciones ópticas, los métodos cada vez son más factibles.

La técnica utilizada (Deflexión de franjas, FD) ha sido comúnmente utilizada para la obtención de la forma de un objeto por comparación con un fondo más claro que él. Su rango de medición va desde unas cuantas décimas de micras hasta unos cuantos milímetros. Las características que hacen a esta técnica tan importante en este tipo de trabajos de investigación es que es un método no invasivo, ya que no entra en contacto físico con el objeto analizado, y por consiguiente es no destructivo, pues no causa ninguna fractura o destrucción del objeto. Finalmente, otra característica de gran importancia es que se trata de una técnica que provee una muy alta sensibilidad, con lo que podemos realizar mediciones en un rango imperceptible a simple vista, aunado a su factibilidad de entregar resultados de campo completo y no sólo en un punto específico del espacio como comúnmente es realizado por los equipos de medición de temperatura industriales.

Ante las facilidades y ventajas que presenta esta técnica, es utilizada para el cálculo de diversas cantidades físicas como gradientes de densidad y de índice de refracción, las cuales están relacionadas con el objeto de estudio de este trabajo: el control de la temperatura.

2.1. Deflexión de rayos

De acuerdo al principio de Fermat, la propagación de un rayo a través de un objeto de fase inhomogéneo está dada por^8-10,

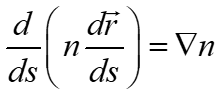, (1)

donde es el vector de posición del rayo para un sistema de referencia establecido, en tanto que s es la longitud de arco de la trayectoria del rayo.

Tenemos pues, que para una dirección de propagación z, el gradiente del índice de refracción sólo se puede registrar en una sola dirección en el plano donde se forma la imagen⁶, en tanto que del lado izquierdo de la expresión (1), el índice de refracción n al mantenerse constante se aproxima al valor del índice del aire n₀ y se puede manejar como una constante.

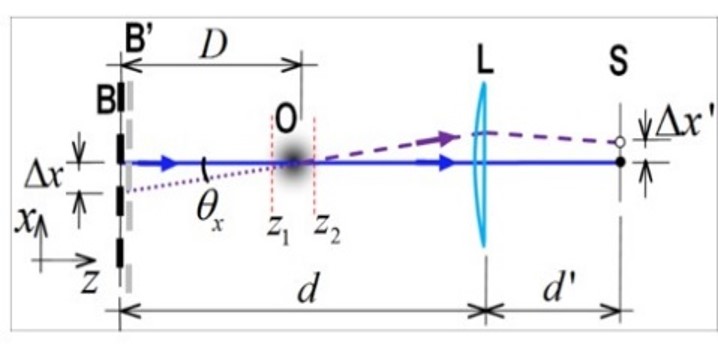
Figura 1. Relación entre la variación del índice de refracción y el corrimiento de las franjas. Imagen de propia autoría¹⁷.

De la Figura 1 podemos observar que la relación correspondiente al ángulo de desviación de un rayo , y asumiendo que el índice de refracción se mantiene constante en la dirección de propagación, es

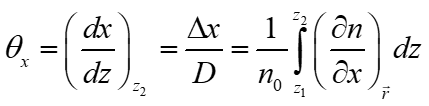, (2)

donde D es la distancia de separación entre el patrón de referencia en el fondo y el objeto de fase, son los desplazamientos aparentes registrados por el sensor de la cámara para la dirección analizada, n₀ el índice de refracción de referencia en el ambiente (aire, para nuestro caso), y dz el cambio en la dirección de propagación de los rayos.

Habiendo tomado en cuenta lo establecido por la ecuación (2), y al ser una función continua e independiente de la dirección z, se puede intercambiar el orden de la integración y la derivada parcial¹⁵.

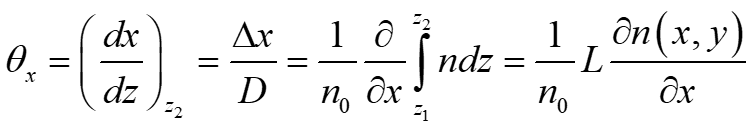.(3)

Por lo tanto, usando la ecuación (3), el índice de refracción y el desplazamiento transversal Δx se relacionan por

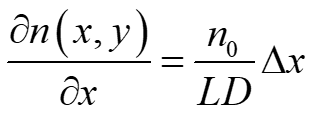, (4)

donde L es la longitud del objeto de fase, D la distancia de separación entre el objeto y el fondo, n₀ el valor de referencia del índice de refracción del aire y Δx los desplazamientos puntuales en toda la región analizada.

Puesto que los desplazamientos son obtenidos a partir del cambio de fase producido por el objeto, éstos están relacionados con el periodo p de las franjas en el fondo, dando origen a la relación entre la variación del índice de refracción y la fase,

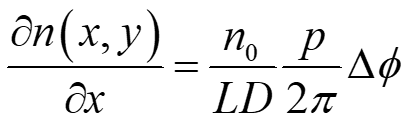. (5)

El cambio en el índice de refracción se calcula al integrar por el método rectangular pixel por pixel¹¹, obteniendo

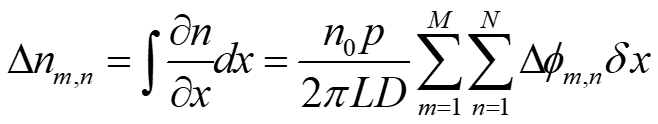, (6)

donde es el tamaño de paso dado al integrar, y se hace la sumatoria para toda la región completa, p es el periodo de las franjas en el fondo, L es la longitud del objeto de fase, D es la distancia de separación entre el fondo y el objeto analizado.

Una vez obtenidos los valores del cambio en el índice de refracción, debemos sumar el índice de refracción del aire n₀ con los valores obtenidos de Δn y así obtener el índice de refracción para cada punto de nuestra región.

2.2. Cálculo del índice de refracción y temperatura

Habiendo obtenido la diferencia de fase entre los estados deformado y de referencia, , los desplazamientos correspondientes son obtenidos mediante la relación,

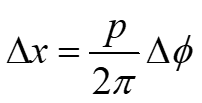, (7)

Ya con los desplazamientos (Δx) y la variación de la fase (Δ ) calculados para toda la región de análisis, ahora se procede a encontrar la variación en el índice de refracción mediante el uso de la ecuación de los gases ideales, y la ecuación de Gladstone-Dale⁶

n — 1=kp (8)

donde k es la constante de Galdstone-Dale para el aire, p es la densidad y n es el índice de refracción en el medio.

La variación del índice de refracción Δn se calcula mediante lo establecido por la ecuación (6) y sumado al índice de referencia del ambiente, n₀.

Para condiciones conocidas de una presión inicial P₀ y para una temperatura ambiente T₀, entonces la ecuación para el cálculo de la temperatura puede ser expresada como

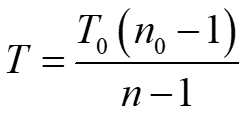, (9)

donde n es el índice de refracción obtenido al introducir el objeto de fase y T la temperatura recuperada para toda la región analizada.

En el estudio de evaluación de los métodos para medición de temperatura es fundamental el análisis de los parámetros y variables que entran en juego al utilizarlos. Se debe conocer la influencia de cada uno en la exactitud y validez de los resultados, así como saber los rangos recomendados en que pueda utilizarse cada parámetro, dependiendo de las condiciones y del equipo de trabajo disponible.

3.1. Generación de índice de refracción gaussiano y decayente exponencialmente

En esta primera parte, se utilizó el software de MatLab¹² para realizar la simulación computacional de la técnica de deflexión de franjas, generando en primera instancia un índice de refracción, cuya forma se encuentra dada por una función gaussiana, de ancho σ= 12.5 mm, en la cual se conocen todos sus valores para cada punto; la región simulada ocupa un espacio de 100x100 mm y cuyo valor máximo de cambio de índice de refracción Δn es de -1.6x10^-4 . Aquí el signo negativo se debe a que en el centro, la flama tiene una mayor temperatura, lo que causa que el índice de refracción Δn disminuya respecto al índice del aire n₀ y, conforme se vaya alejando, la temperatura va siendo menor y el n₀ sufre menos cambio, como lo muestra la figura 2b.

Como se analizó previamente, se utiliza un índice de refracción gaussiano decayente exponencialmente en la dirección vertical, dado por la expresión,

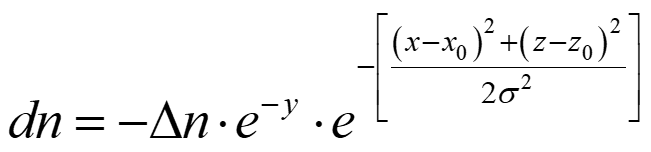, (10)

donde Δn es la máxima amplitud del cambio de índice de refracción, el término e^-y proporciona el decaimiento exponencial en la dirección vertical y σ el ancho del perfil gaussiano.

La figura siguiente muestra la variación del índice de refracción generado, dn.

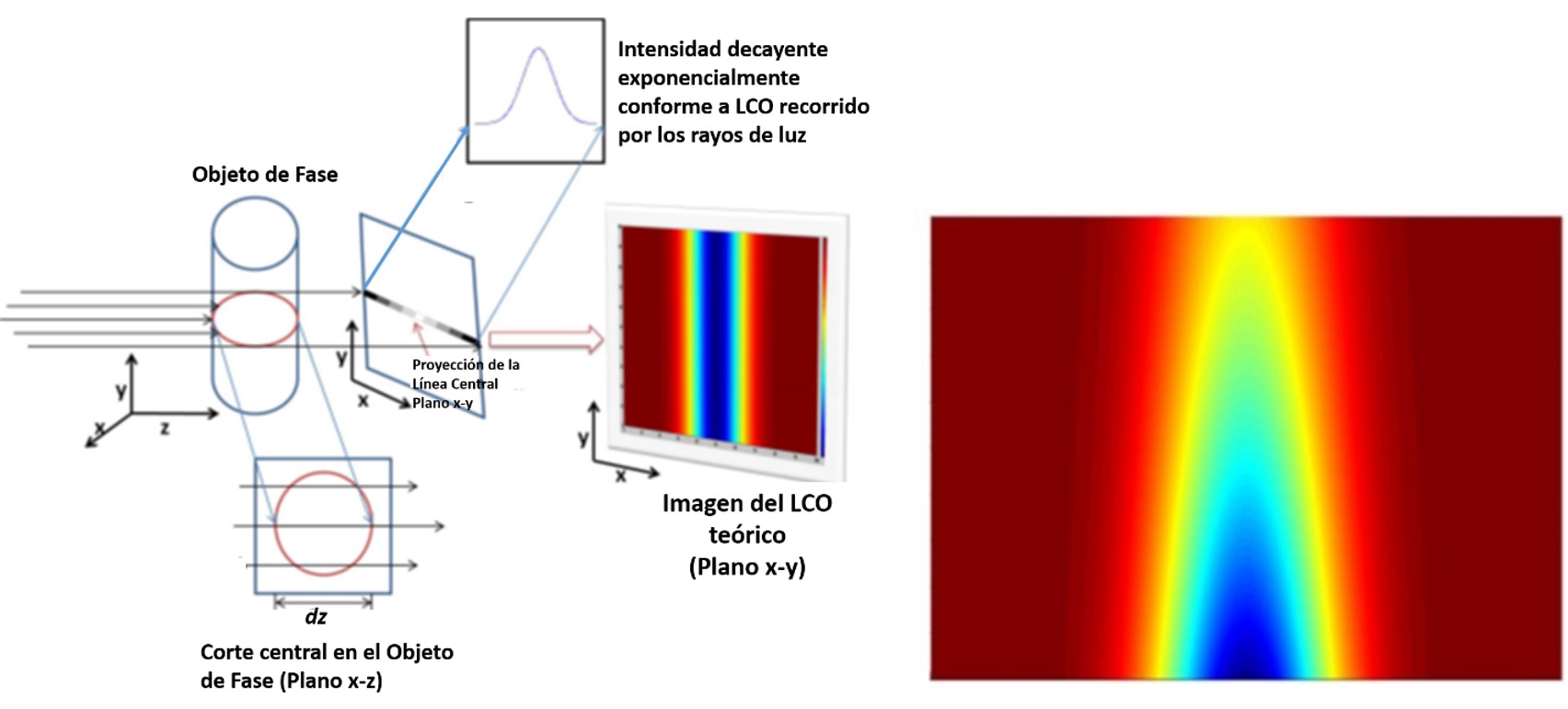
Figura 2. a) Longitud de camino óptico recorrido por los rayos de luz. b) dn generado (región de 100x100mm (1280x1024 pixeles) con un máximo de -1.6x10^-4).

Para el fondo de referencia (estado inicial sin objeto de fase con patrón periódico de referencia) se generaron imágenes con un patrón de 100 franjas senoidales, dando origen a un periodo de 1mm/franja con un ciclo de trabajo 50-50 (Figura 5a). Nuevamente sobre estas imágenes generadas numéricamente se aplica el método de Fourier^13-14 a fin de recuperar los parámetros analizados (fase, desplazamientos, índice de refracción y temperatura) y así realizar la comparación con los valores teóricos y analizar la precisión de la técnica.

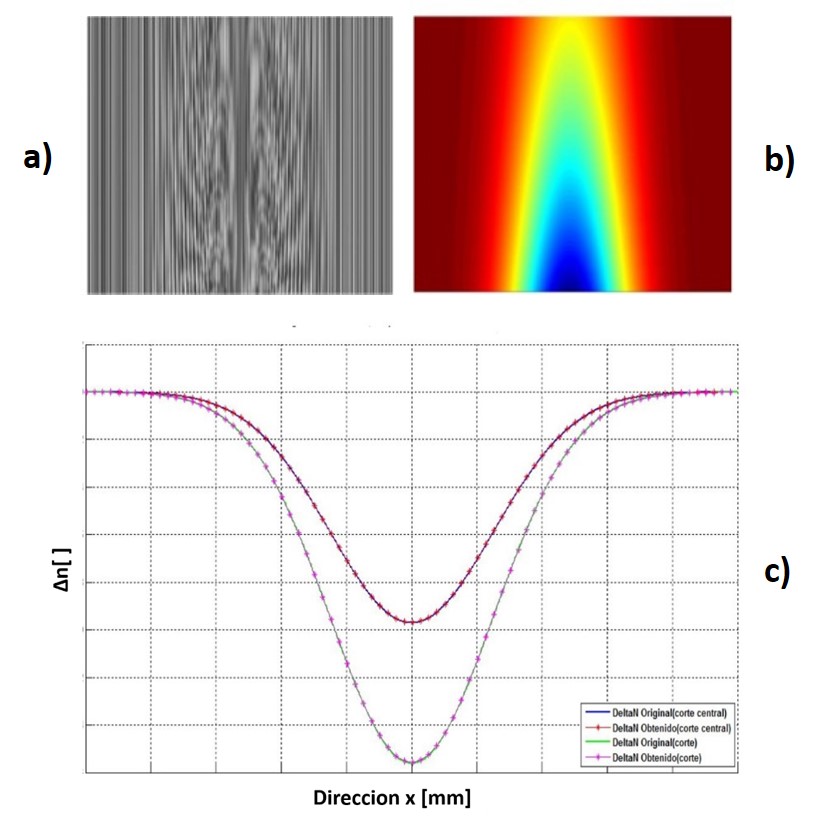
Figura 3. a) Patrón de franjas deformado. b) Índice recuperado. c) Perfiles de comparación entre índice generado e índice recuperado mediante la implementación de la técnica analizada (obteniendo un error relativo porcentual de 8.2x10-6 %), cortes en la dirección horizontal de la figura 3b. La escala horizontal está en mm (0-100), la escala vertical es adimensional (0 – 1.6x10^-4).

Con estos valores recuperados, y haciendo uso de la ec. (8), los valores para la temperatura puntual en toda la región son calculados, obteniendo un error relativo porcentual respecto a los valores teóricos generados de 0.04%.

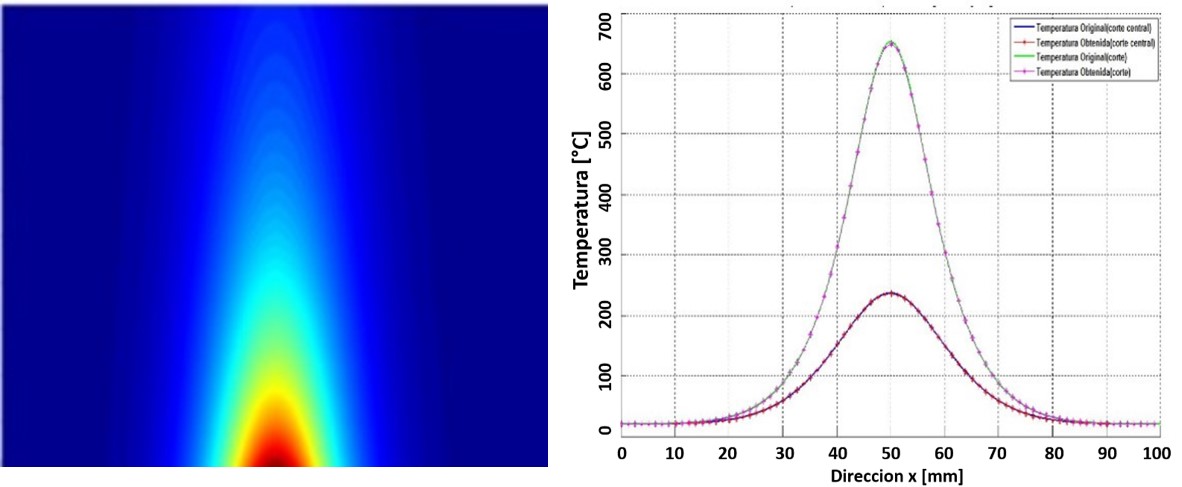
Figura 4. Temperatura recuperada. a) Vista completa. b) Perfiles de comparación (cortes en la dirección horizontal de la figura 4a).

Después de visualizar la validez de la técnica de deflexión de franjas y su capacidad de medición para la variable física analizada (temperatura) se procedió a su implementación experimental bajo condiciones controladas y en ambientes industriales reales.

En este apartado se describe el procedimiento experimental aplicado para cada una de las mediciones realizadas. Se explica detalladamente el arreglo, sus características y se reportan los resultados experimentales para verificar su efectividad en los propósitos requeridos. Además se presenta la medición realizada en un dispositivo eléctrico comercial para verificar la utilidad de esta técnica en aplicaciones industriales.

4.1. Arreglo experimental

La figura 5 muestra un arreglo esquemático con los componentes a ser utilizados en el montaje experimental.

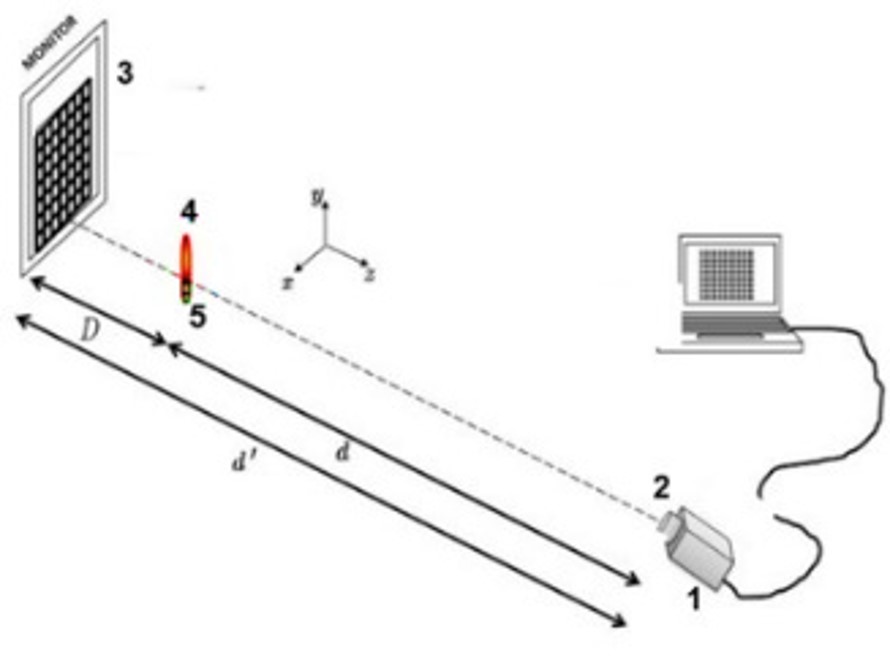
Figura 5. Montaje esquemático para la técnica de deflexión de franjas. 1. Cámara CCD, Lumenera 2/3” modelo Lu165 (1024x1280 pix). 2. Lente telefoto Canon con zoom variable (70-300 mm), funcionando a un f/16, con un tiempo de exposición de 30 ms y 15 fps. 3. Monitor Dell Ultra Sharp 2007FP (1766x1050 pix). 4. El objeto de fase, la flama a la salida de un soplete de gas butano a una presión controlada (35kPa). 5. Regulador de presión CORTEC para gas acetileno.)

La distancia del CCD a la pantalla del monitor fue de 4.3 m, con lo cual las desviaciones de los rayos θ_x son pequeñas, cumpliendo así el concepto de la aproximación paraxial¹⁵ establecido en la ecuación (2), como se mencionó en la sección de análisis matemático. El objeto de fase se colocó a 70 cm respecto al monitor. La región de observación resultante fue de 13x11 cm. En el plano del monitor se obtuvo un periodo de franja de 1.5 mm.

4.2. Objeto de fase: flama de soplete de gas butano

En la figura 6a se muestra el mapa de franjas deformadas por la presencia de la flama del soplete; la resta de los estados de referencia y deformado se ilustra en la figura 6b.

Figura 6. Patrón de franjas: a) deformadas, b) resta.

Así, mediante estas imágenes se calcula el mapa de fase mostrado en la figura 7a.

El mapa de fase generado origina un desplazamiento Δx máximo de 7x10^-4 m (figura 7b), lo cual corresponde a que el valor inicial del índice de refracción (figura 7c) se reduzca a 1.00004.

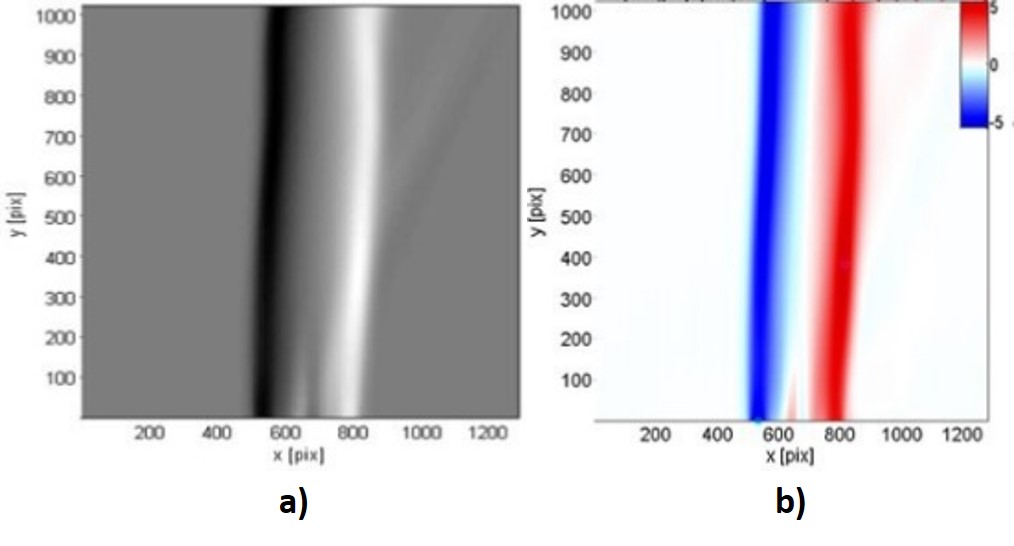
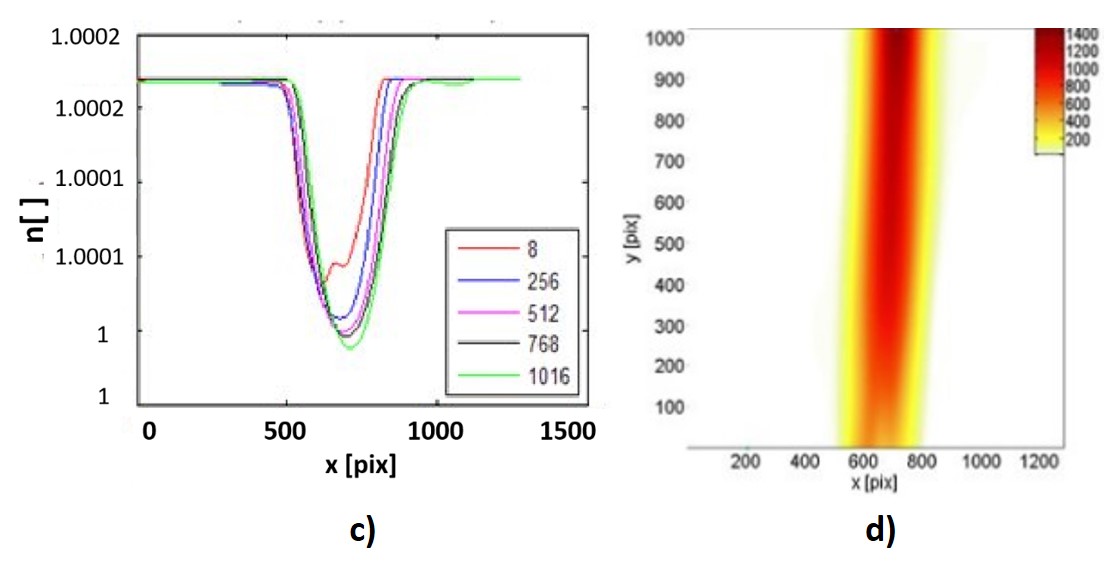
Figura 7. a) Fase obtenida (valor máximo de 2.3 rad). b) Δx obtenido. c) Perfiles horizontales del índice de refracción obtenido. d) Temperatura obtenida (valor máximo de 1317.9 °C) y mapa de colores en escala de grados centígrados.

Los resultados fueron comparados con las mediciones obtenidas mediante un termopar tipo R con recubrimiento de cerámica para altas temperaturas, esto con la finalidad de tener 5 puntos de referencia mediante una medición directa como cotidianamente se realiza en ambientes industriales, y así poder calcular el error relativo porcentual correspondiente en el punto analizado (ver la Tabla 1).

Tabla 1. Comparación de resultados experimentales y tomados con termopar a diferentes alturas de la flama.

Posición [cm]	Termopar	Deflexión de Franjas	Error
1	1670	1697.8	1.7 %
2.1	1620	1670.5	3.1 %
3.6	1602	1630.2	1.7 %
4.8	1570	1600.5	1.9 %
5.5	1525	1568.4	2.8 %

Como se puede observar, el error relativo porcentual encontrado respecto a los valores generados en la técnica de FD es del 1.7 % para la posición seleccionada, con lo cual se puede afirmar con toda certeza su gran potencial de aplicación para desarrollo tecnológico e industrial, ya que es capaz de registrar variaciones de temperatura debidas a cambios de índice de refracción en medios homogéneos, aun cuando existe un flujo de aire a alta velocidad.

4.3. Aplicación en una secadora comercial de ropa

Como consecuencia de los análisis previos^16-17, se pretende extender la aplicación de la técnica dentro de un ambiente industrial, y para ello se solicitó apoyo del Centro de Investigaciones en Óptica, donde se contaba con un prototipo de secadora comercial de ropa, para su análisis en la medición de temperatura dentro de su tambor. Se presentan resultados preliminares de medición de temperatura del aire caliente que circula en una secadora eléctrica doméstica.

De los mapas de temperatura obtenidos se observa un nivel alto de turbulencia; esto está básicamente asociado a los valores de velocidad del aire dentro del tambor, los cuales están alrededor de 0.6 m/s, esto se traduce en un análisis posterior que debe ser involucrado como lo es la medición simultánea del parámetro de velocidad y flujo volumétrico.

Adicionalmente, se aprecia que la temperatura desciende de 50 a 30 °C en una distancia de 20 cm, en la región de entrada de la secadora, es decir, justo después de pasar la zona de resistencias eléctricas (elemento calentador de aire). El área de observación fue de 32x20 cm².

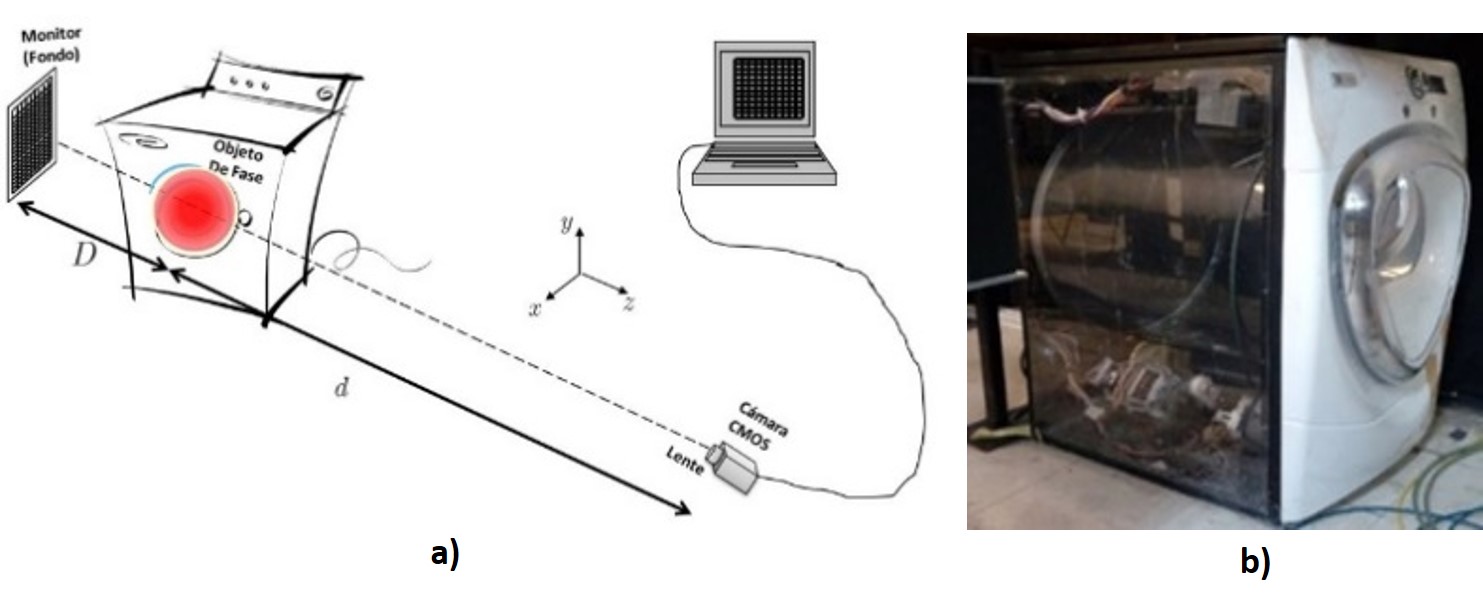
Figura 8. a) Representación esquemática del arreglo experimental (cámara Lumenera Lt225C (2048x1088 pix), monitor Dell Ultra Sharp 2007FP (1766x1050 pix), lente telefoto Canon (zoom 70-210 mm), D=1 m, d= 4.17 m, L=0.8 m). b) Prototipo de secadora comercial de ropa, diseñada para la toma de imágenes.

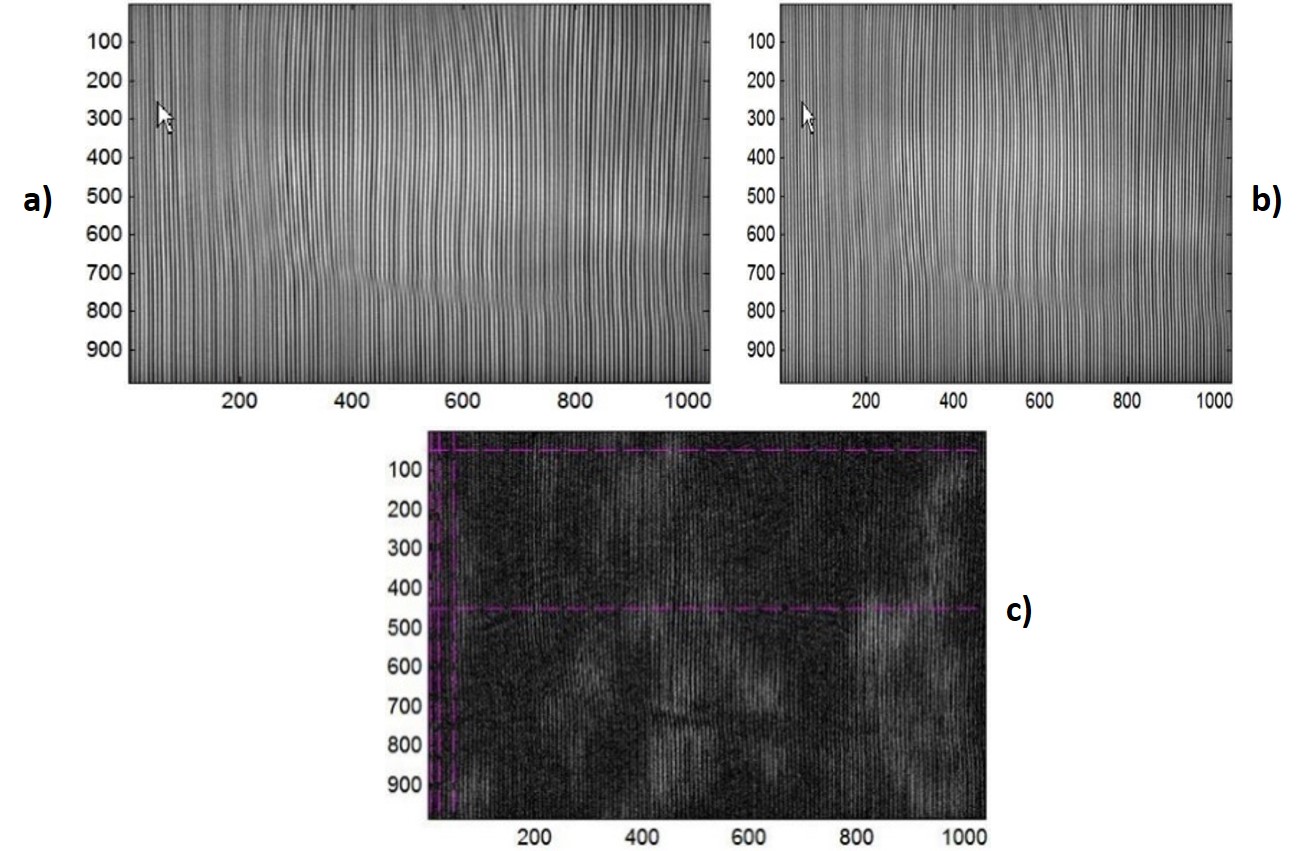
Figura 9. a) Imagen de referencia. b) Imagen deformada. c) Sustracción de imágenes. Escalas en pixeles para ambos ejes.

Figura 10. a) Filtros pasa-bandas aplicados a la imagen de referencia y deformada. b) Fase Desenvuelta recuperada del lóbulo horizontal mostrado en color cian (escalas x,y en pixeles).

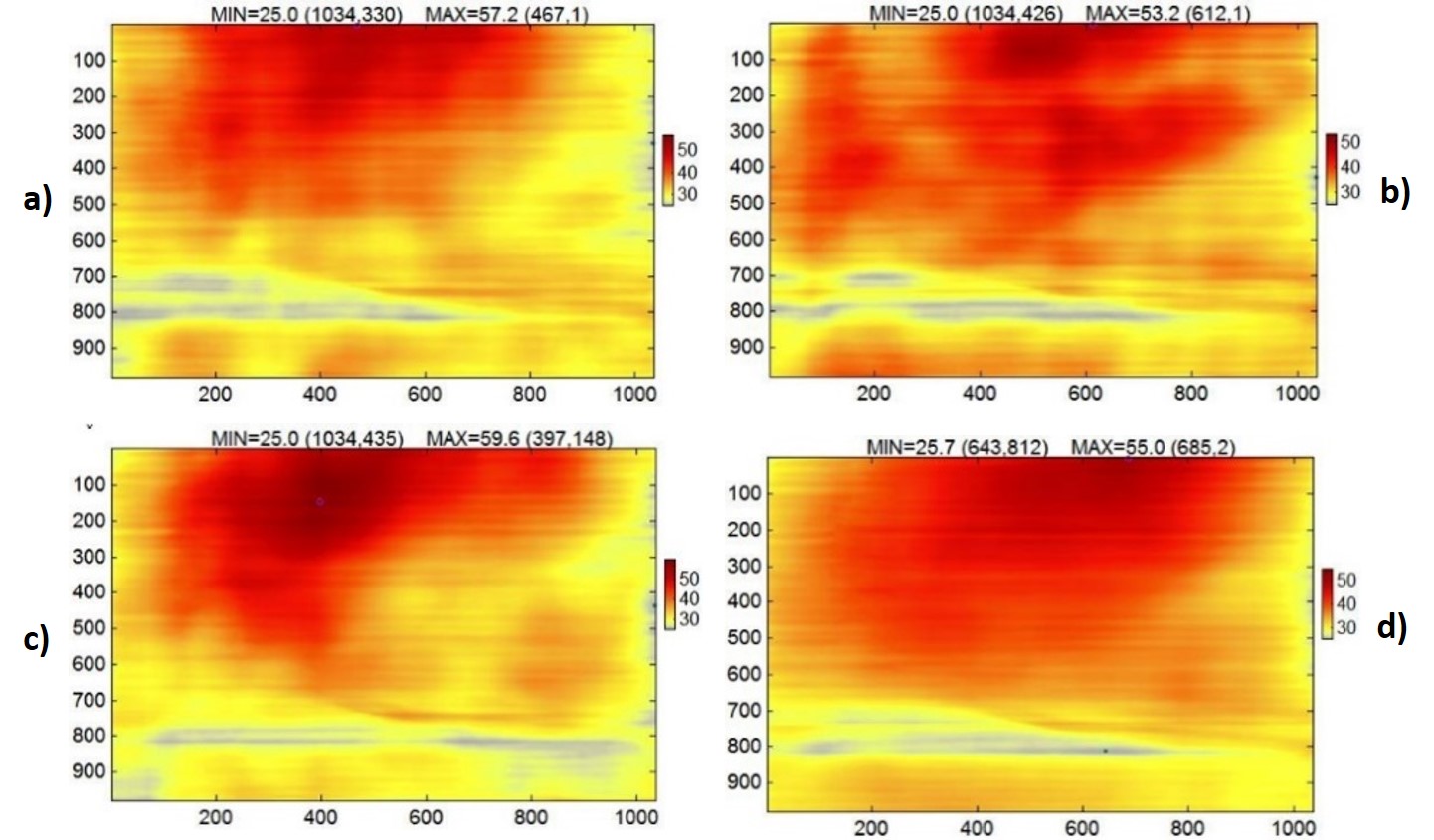
Figura 11. Evolución temporal de la temperatura en la región analizada. a) Temperatura obtenida (t=5s); b) Temperatura obtenida (t=15s); c) Temperatura obtenida (t=20s); d) Temperatura obtenida promedio de 10 imágenes (Δt = 60s). Las escalas de los ejes horizontal y vertical están en pixeles. El mapa de colores muestra la temperatura en escala de grados centígrados.

Con el fin de complementar la información aquí presentada, se realizaron estudios para la empresa Mabe, logrando resultados lo suficientemente válidos implementando un sistema de medición de los 3 parámetros físicos (temperatura, flujo volumétrico y velocidad) para un fenómeno transitorio. Los análisis y pruebas realizadas no se presentan debido a su carácter de confidencialidad para la empresa mencionada.

Figura 12. Herramientas tecnológicas instaladas en Mabe, a) para gasto volumétrico (izquierda) y b) velocidad (derecha).

En este trabajo se mostró la factibilidad de la técnica óptica FD para la medición de temperatura. Respecto a la sensitividad a ruido externo, resulta prometedora por el hecho de usar luz blanca. Además la señal de información puede ser diseñada a voluntad y en forma expedita, esto último gracias al uso de un monitor LCD donde se generan las franjas.

El tiempo que le lleva el procesamiento de la información es muy corto, y debido a que las franjas de FD contienen niveles relativamente bajos de ruido, éstas pueden ser procesadas mediante un algoritmo de desenvolvimiento extremadamente sencillo.

Se puede también concluir que, aunque se basa en el cálculo de la derivada del índice de refracción, los resultados que entregan son de una muy alta calidad y certeza. Esto se tiene sobre todo cuando la variación del índice de refracción corresponde a una función gaussiana, en cuyo caso los valores puntuales dentro de la flama son proporcionales a los proyectados y con ello también se evita usar métodos de desproyección.

Para el procedimiento experimental cabe puntualizar también que fue necesario saber la temperatura sólo en dos puntos (el máximo y la de los alrededores, por ejemplo) para obtener la temperatura en todo el volumen.

Aunado a esto, y ampliando su campo de aplicación, la prueba se realizó en el tambor de una secadora comercial de ropa, entregando resultados de temperatura que al ser comparados con los valores máximos registrados por un termopar en un punto de la región analizada registraron un error relativo del 3.8 % para una sola imagen, y del 6.5 % para un promedio de imágenes obtenidas en el lapso de un minuto.

Sobre la base de estos resultados podemos darnos cuenta que además de ser una técnica no invasiva, nos permite observar la distribución de temperatura en un dispositivo, lo cual para fines de diseño y manufactura permitiría tener una mayor eficiencia en el consumo de energía eléctrica.

1. PINTO, J. M. Medición interferométrica de temperatura de una llama axisimétrica. Tesis de Maestría en Ciencias de la Ingeniería, Pontificia Universidad Católica de Chile, Santiago de Chile. Julio 2007.
2. ALVAREZ-HERRERA, C., MORENO, D. and BARRIENTOS, B. Temperature measurement of an axisymmetric flame by using a schlieren system, J. Opt. A: Pure Appl. Opt., (10), 104014. Agosto 2008.
3. ALVAREZ-HERRERA, C., MORENO, D., BARRIENTOS, B. and GUERRERO Viramontes, J. A. Temperature measurement of air convection using a schlieren system. Opt. Laser Tech. (41): 233-240. Abril 2009.
4. SHAKHER, C., NIRALA, A. K., PRAMILA, J. and VERMA, S. K. Use of speckle technique for temperature measurement in gaseous flame. J. Optics 23(2): 35-39. Marzo 1992.
5. XIAO, X., CHOI, C. W. and PURI, I. K. Temperature measurement in steady two dimensional partially premixed flames using laser interferometric holography. Combustion and Flame (120): 318-332. Febrero 2000.
6. JENSEN, O. S., KUNSCH, J. P. and ROSGEN, T. Optical density and velocity measurements in cryogenic gas flows, Experiments in Fluids (39): 48-55. Mayo 2005.
7. HAUF, W. and GRUGULL, U. Optical Methods in Heat Transfer, pp. 166-167, Academic Press Inc. New York (1970).
8. DORIC, S. Ray tracing through gradient-index media: recent improvements. Applied Optics. (29): 4026-4029. Enero 1990.
9. HAZEWINKEL, J., MAAS, L. R. M. and DALZIEL, S. B. Tomographic reconstruction of internal wave patterns in a paraboloid. Experiments in Fluids (50): 247-258. Febrero 2011.
10. RICHARD, H. and RAFFEL, M. Principle and applications of the Background Oriented Schlieren (BOS) method. Measurement Science and Technology (12): 1576-1585. Agosto 2001.
11. DAVIS, J. and RABINOWITZ, Philip. Methods of Numerical Integration. Academic Press Inc. New York, 1984, pp. 51-52. ISBN 0486453391.
12. LEIS, John W. Digital Signal Processing using Matlab for Students and Researchers. 2011, p. 82. ISBN 9781118033807.
13. TAKEDA, M., INA, H. and KABAYASHI, S. Fourier-Transform Method of Fringe-Pattern Analysis for Computer-Based Topography and Interferometry. Journal of the Optical Society of America (1): 156-160. Enero 1982.
14. VANLANDUIT S.et al., Fourier fringe processing by use of an interpolated Fourier-transform technique, Applied Optics. (43): 5206–5213, Septiembre 2004.
15. JENKINS F. A. and WHITE, H. E. Fundamentals of Optics. McGraw-Hill, 1976. ISBN 0070323305.
16. BLANCO, A., BARRIENTOS, B. and MARES, C. Performance comparison of background-oriented schlieren and fringe deflection in temperature measurement: part I. Numerical evaluation. Optical Engineering. 55(5): 054102. Mayo 2016.
17. MARES, C., BARRIENTOS, B. and BLANCO, A. Measurement of transient deformation by color encoding. Opt. Express 19(25): 24838-25842. Diciembre 2011.