Este artículo presenta el modelado matemático no lineal de un automóvil utilitario, tomando en cuenta la dinámica de la velocidad longitudinal, velocidad lateral y velocidad angular de viraje o yaw. Estas dinámicas se simularán en simulink con las normas ISO 3888-1 e ISO 7401 que servirán como plataforma para el uso del CarSim, el cual es un software que simula el comportamiento dinámico de cualquier tipo de automóvil y las simulaciones arrojadas son vistas en 3-D. Además de establecer estas simulaciones como herramientas de diseño para la industria automotriz.

Palabras Clave: Automóvil, Simulación, CarSim.

This article presents the nonlinear mathematical modeling of a utility vehicle, taking into account the dynamics of longitudinal velocity, lateral velocity and angular velocity of yaw. These dynamics will be simulated on Simulink with the norms ISO 3888-1 and ISO 7401 that will serve as a platform for the use of CarSim, which is a software that simulates the dynamic behavior of any type of automobile and the simulations thrown are 3-D views. In addition to establishing these simulations as design tools for the automotive industry.

Keywords: Automobile, Simulation, CarSim.

En los últimos años, el desarrollo de una filosofía integral ha cambiado la forma de investigación en el área de diseño de nuevos dispositivos para el control del automóvil. Actualmente se cuenta con gran potencia computacional que permite trabajar con unidades de control en los vehículos, debido al mejoramiento de dispositivos electrónicos y al avance en la tecnología que permiten desarrollar nuevos sistemas de control que evitan cualquier restricción desde el punto de vista tecnológico.Considerando algunas variables físicas del automóvil, el diseño de un sistema de control para la velocidad lateral es uno de los principales tópicos de investigación en el área de control de automóviles.

Estos dispositivos modifican las dinámicas de los vehículos imponiendo fuerzas o momentos en el cuerpo del automóvil de diferentes maneras^{1,2,3,5,9,10,11}, y también pueden utilizar “sensores inteligentes” que permiten mediciones precisas de las variables que se desean medir con alta eficiencia en la acción que el controlador esté realizando, lo que contribuye a la estabilidad del vehículo, la seguridad y confort para la persona que conduce^7,13.

El movimiento de un vehículo puede ser categorizado en términos de su funcionalidad, así como de su maniobrabilidad y estabilidad. El funcionamiento está enfocado sobre el peso y los movimientos longitudinales del chasis; la estabilidad y las características de manejo generalmente se refieren a la respuesta lateral/maniobrabilidad de las acciones de conducción del automóvil que se requieran^4,14. Una gran variedad de modelos de bajo, medio y alto orden están disponibles para describir el movimiento traslacional y rotacional del automóvil. Un modelo del vehículo de bajo orden de un grado de libertad (DOF por sus siglas en inglés) donde el automóvil considera una masa puntual y con ello, es suficiente para generar una plataforma de velocidad. Un modelo de dos grados de libertad es considerado de medio orden por su análisis¹², teniendo en cuenta que las llantas frontales y traseras del vehículo son tomadas como una sola llanta delantera y una trasera (modelo de la bicicleta). En este modelo, en la llanta delantera se puede introducir la dinámica del conductor y del volante; además, los efectos del ángulo roll y de transferencia de masa son despreciados lo que permite estudiar la respuesta lateral/dirección del vehículo para pequeños ángulos de maniobrabilidad en velocidades longitudinales. Este artículo presenta el modelo matemático de alto orden y la transferencia de masa del mismo sistema; todos estos parámetros deben ser medidos para la completa realización a futuro de algunos diseños⁸. Esta medición de parámetros físicos se pueden realizar mediante la utilización de un software como el CarSim, el cual ofrece una amplia gama de soluciones tanto para el tratamiento de datos como para la simulación en una manera visual muy agradable; además de obtener gráficas de cada una de las variables físicas a medir, también considera las características del automóvil como la altura del mismo con respecto a un centro de gravedad, las longitudes frontal y trasera con respecto a las llantas y al centro de masa. Otra característica importante de este software llamado CarSim es que puede relacionarse con el programa Matlab-simulink, conocido por diseñadoras/es, investigadoras/es y estudiantes de ingeniería, obteniendo grandes aplicaciones a niveles de investigación tanto en educación como en la industria.

Una de las aplicaciones es la implementación de algoritmos de control para el automóvil y enviarlos al CarSim para simularlos y corroborar si son correctos, ahorrando tiempo y dinero, por lo que esta herramienta, a nivel mundial, es importante en el diseño automotriz. Este artículo de investigación comienza por la sección dos, donde se muestra el modelo matemático del vehículo a utilizar con sus dinámicas revisadas; en la parte tres, se establecen las simulaciones del comportamiento del modelo matemático del automóvil y se observa la interconexión del Matlab-Simulink con el CarSim y por último, se presentan las conclusiones y las referencias.

El modelo dinámico (Figura 1) presentado en esta sección es usado en las simulaciones numéricas para estimar valores del automóvil. En ecuación (1) se muestra el modelo matemático del vehículo utilizado para la simulación que considera tres grados de libertad; la velocidad longitudinal, la velocidad lateral y la velocidad angular yaw, pueden expresarse usando el llamado modelo de la bicicleta¹;

(1)

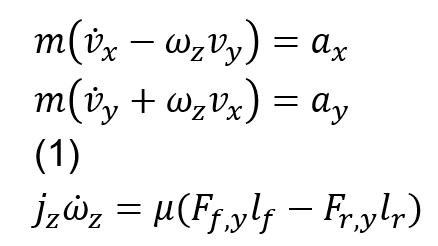
Donde m,j_z son la masa y la inercia del vehículo con respecto al eje perpendicular; x,y,l_f,l_r son las distancias desde el centro de gravedad del vehículo (CG) a la llanta frontal y trasera; a_x,a_y son la aceleración longitudinal y lateral; v_x,v_y son las velocidades longitudinal y lateral del CG; ω_z es la velocidad angular yaw; μ es el coeficiente de fricción. Además F_(f,y,F_r,y son las fuerzas laterales frontales y traseras de las llantas respectivamente y se supone que se tiene un coeficiente de fricción alto entre las llantas y el suelo.

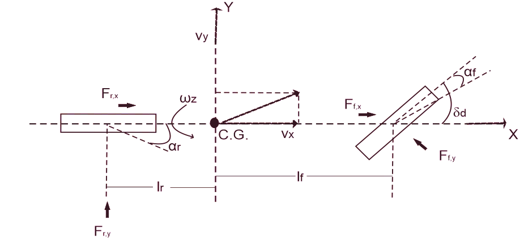
Fig. 1. Modelo no lineal de la bicicleta.

De (1) se obtiene el sistema dinámico;

(2)

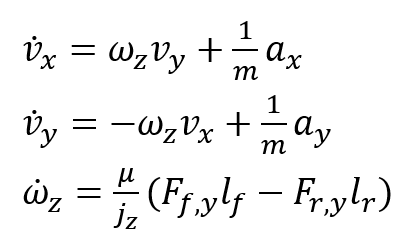
Este modelo describe las dinámicas del vehículo bajo las siguientes consideraciones:

• Dinámica pitch no considerada.
• El sistema es rígido.
• La suspensión es pasiva.

Las aceleraciones longitudinal a_x y lateral a_y en (2) pueden ser expresadas en términos de las fuerzas del neumático longitudinal y lateral;

(3)

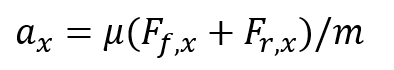
(4)

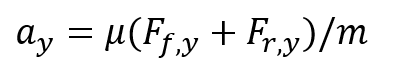
Y pueden ser medidas por acelerómetros usualmente a bordo de automóviles modernos. En donde F_f,x,F_r,x son las fuerzas longitudinales del neumático frontal y trasera. Las fuerzas longitudinal y lateral pueden ser definidas mediante la siguiente fórmula mágica de Pacejka;

(5)

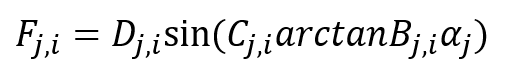
Con i=x,y,j=f,r. Las constantes B_j,i,C_j,i,D_j,i en (5) son experimentalmente determinadas (ver Tabla 1). El ángulo de deslizamiento de los neumáticos α_f,α_r definidos como Di Cairano⁶;

(6)

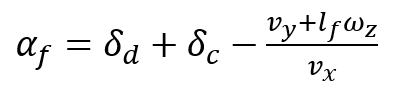
(7)

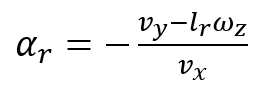
Donde δ_d el ángulo de la rueda,δ_c componente del ángulo de control impuesto a la llanta delantera.

Tabla 1. Parámetros reales usados en la simulación del vehículo.

El comportamiento del modelo matemático del automóvil se simula (Simulink- Matlab-CarSim), bajo una maniobra ISO 3888-1, también conocida como “double change” con un ángulo δ_d, que se muestra en la Figura 2.

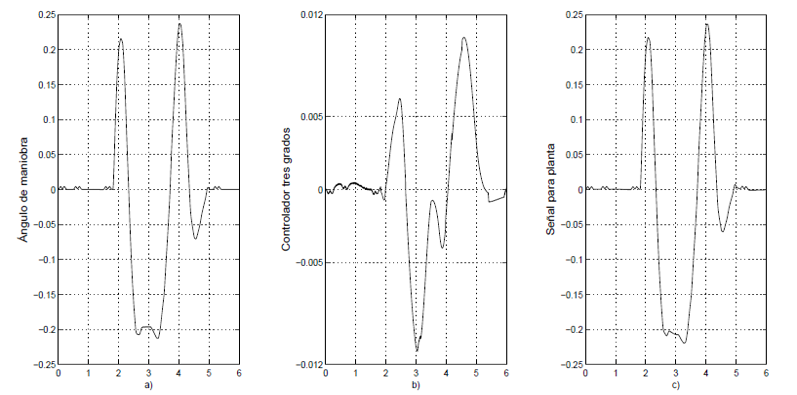
Fig. 2. a) δ_d (rad vs s); b) δ_c (rad vs s); c) δ=δ_d+δ_c (rad vs s).

En este modelo matemático en ecuación (2), la simulación de la velocidad angular yaw controlada con respecto a un sistema de referencia se puede ver en la Figura 3.

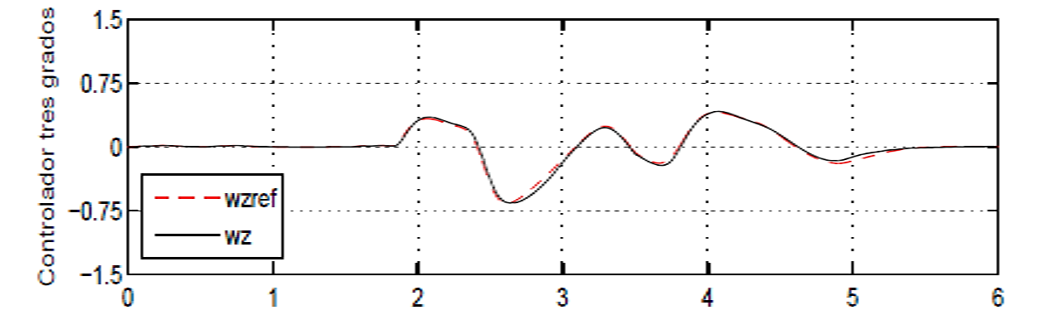
Fig. 3. Velocidad angular de viraje ω_z (rad vs s).

La simulación de la velocidad lateral controlada con respecto a un sistema de referencia se muestra en la Figura 4.

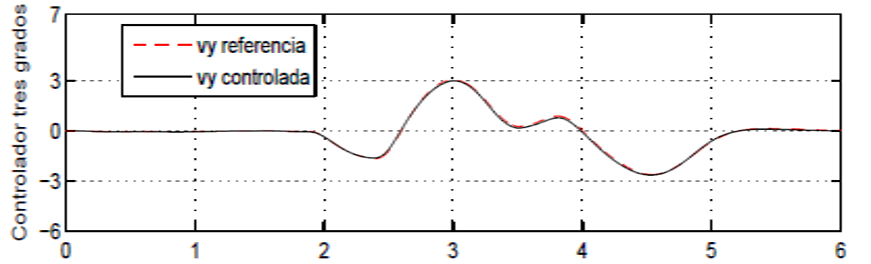
Fig. 4. Velocidad lateral v_y (m/s vs s).

Maniobra ISO 7401, también conocida como “Escalón” con un ángulo δ_d, que se muestra en la Figura 5, la simulación de la velocidad angular en la Figura 6 y la simulación de la velocidad lateral en la Figura 7.

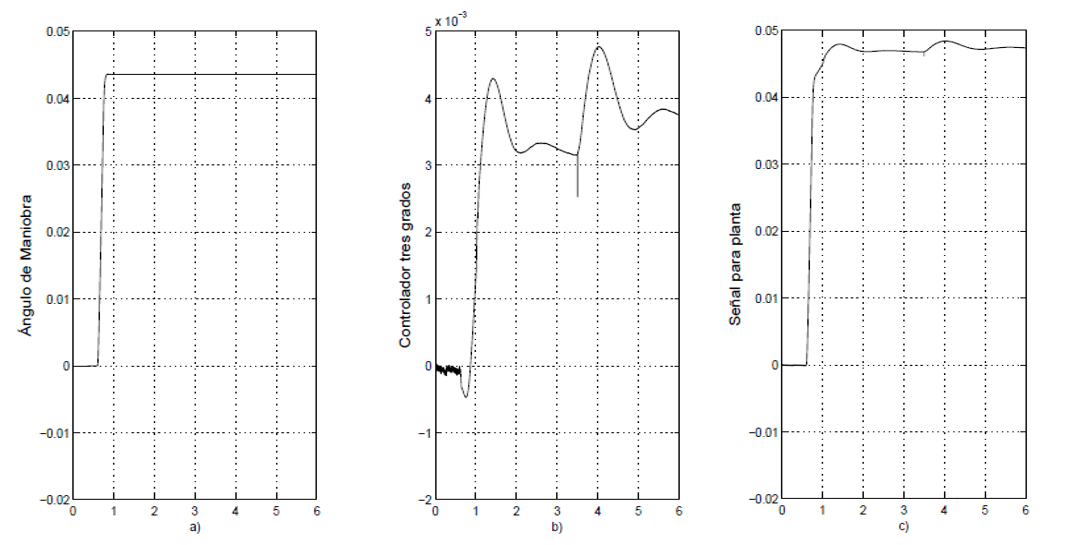
Fig. 5. a) δ_d (rad vs s); b) δ_c (rad vs s); c) δ=δ_d+δ_c (rad vs s).

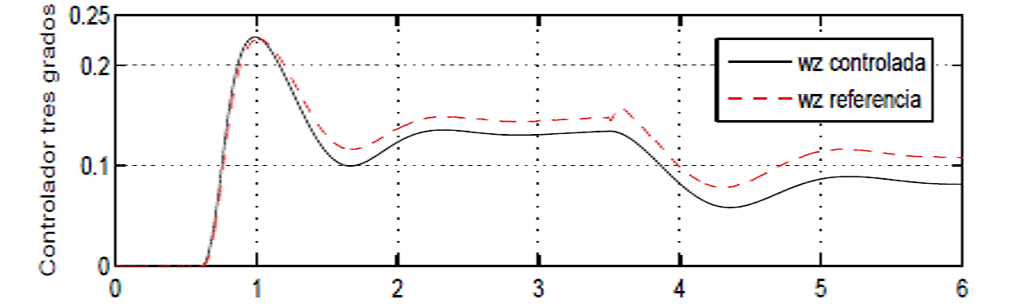
Fig. 6. Velocidad angular de viraje ω_z (rad vs s).

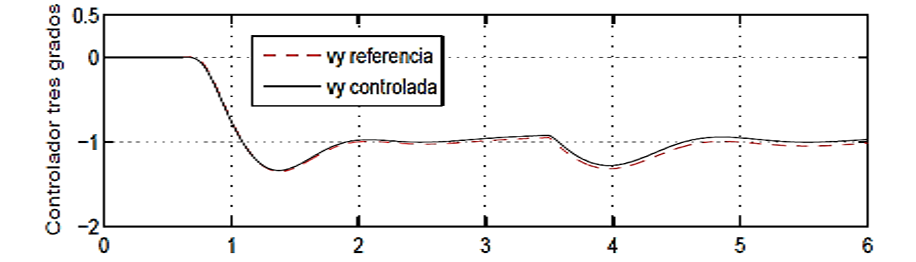
Fig. 7. Velocidad lateral v_y (m/s vs s).

La forma de interconectar el Matlab-Simulink con el CarSim, se observa en la Figura 8. El inicio del software CarSim ofrece la siguiente pantalla:

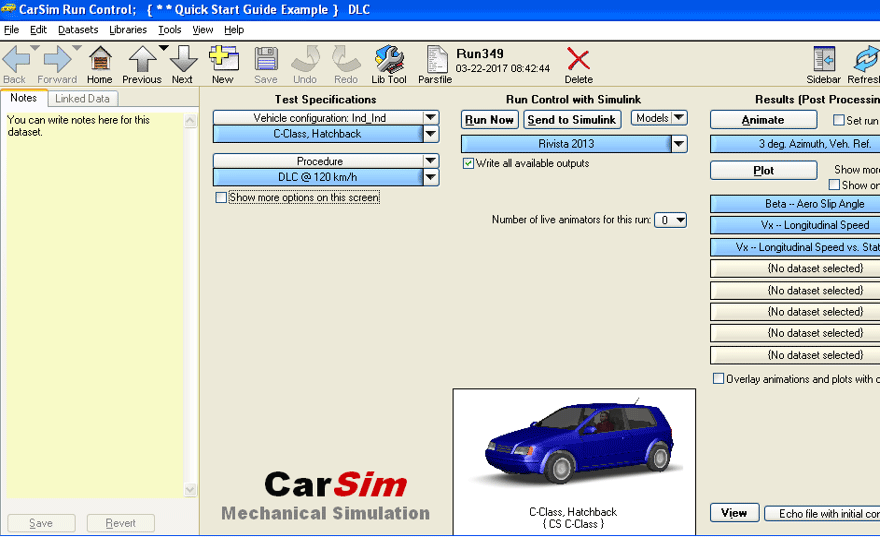
Fig. 8. Panel frontal del software CarSim-Simulink.

A continuación, se trabaja con la programación de los algoritmos del automóvil (análisis matemático), se empiezan a programar los blocks en Simulink, estos valores son los que se utilizan para el modelo matemático del vehículo (ver Figura 9), teniendo en cuenta que se envían al software CarSim para su evaluación como se muestra en Figura 10.

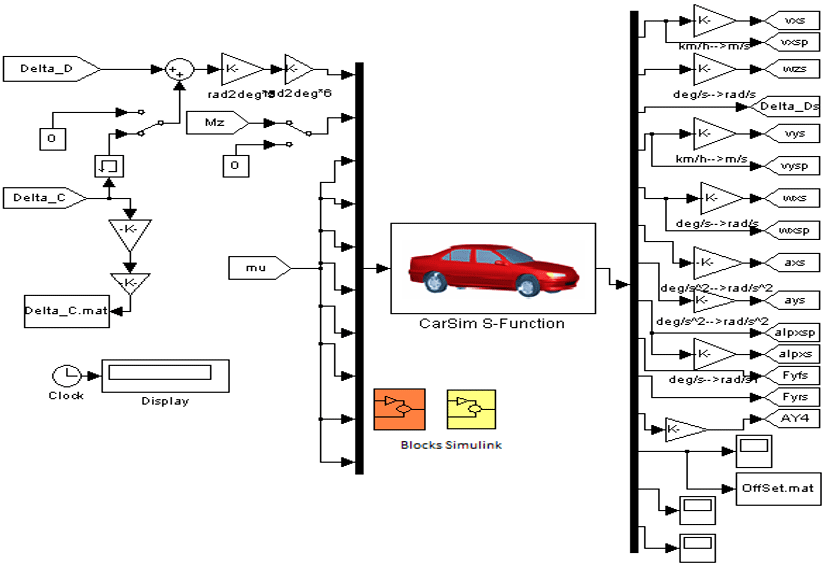
Fig. 9. Programación Simulink-CarSim.

Fig. 10. Simulación en software CarSim.

En este trabajo de investigación se propuso un modelo no lineal de tres grados de libertad para el automóvil aplicando un control activo en Matlab-simulink para obtener las dinámicas del vehículo controladas, comparando con un modelo de referencia que proporciona las variables del automóvil en condiciones ideales (llantas nuevas, suspensión nueva, etc.). Todos los algoritmos matemáticos tanto para el controlador como para el sistema de referencia no se analizaron porque se solo presentó el funcionamiento del software CarSim, dado que tiene una aplicación para simulación de los modelos matemáticos de controladores que se diseñan; se pudo observar que funcionan correctamente en la parte de aplicación física a futuro en el vehículo. También, por diferentes teorías de control se pueden proponer observaciones para las dinámicas del automóvil y aplicarlas al software CarSim y ver su funcionalidad. Se obtuvo como conclusión que a partir de un modelo matemático sencillo de control se pueden realizar aplicaciones al simulador y definir diseños para aplicaciones como pueden ser a direcciones asistidas para la estabilidad y maniobrabilidad en el automóvil. Por último, cabe mencionar que este tipo de investigaciones favorecen que el estudiantado mexicano se inicie en el campo del diseño automotriz para lograr los centros de investigación necesarios en la actualidad.

Símbolos

m Masa del vehículo (kg)

j_z Momento de inercia del Vehículo (kg m²)

l_f,l_r Longitud desde el centro del vehículo hacia la llanta frontal y trasera (m)

v_x Velocidad longitudinal (m/s)

v_y Velocidad lateral (m/s)

ω_z Velocidad angular yaw del vehículo (rad/s)

α_f,α_r Ángulo de deslizamiento lateral de las llantas frontal y trasero (rad/s)

δ_d Componente del ángulo de la llanta impuesto por el conductor (rad)

ω_z Velocidad angular yaw del vehículo (rad/s)

F_f,y, F_r,y Fuerzas frontal y trasera lateral de las llantas (N)

F_f,x, F_r,x Fuerzas frontal y trasera longitudinal de las llantas (N)

a_x, a_y Aceleración longitudinal y lateral (m/s²)

1. ACOSTA, C, DI GENNARO, S, SÁNCHEZ Maria. An Adaptive controller applied to an anti-lock braking system laboratory. Revista DYNA de la Universidad Nacional de Colombia, Vol. 83, 2016, p. 69-77. ISSN # 0012-7353.
2. ACKERMANN, J, GULDNER, J, STEINHAUSNER, R, UTKIN, V. Linear and nonlinear design for robust automatic steering. IEEE Transactions on Control System Technology, Vol. 3, 1995, No. 1, p. 132-143.
3. BASLAMISLI, S. C, POLAT, I, Kose, I. E. Gain Scheduled Active Steering Control Based on a Parametric Bicycle Model. IEEE Intelligent Vehicles Symposium, 2007, p.1168-1173.
4. BIANCHI, D, BORRI, A, Di BENEDETTO, M. D, Di GENNARO, S, BURGIO, G. Adaptive Integrated Vehicle Control Using Active Front Steering and Rear Torque Vectoring. International Journal of Vehicle Autonomous Systems, Special Issue on: “Autonomous and Semi-Autonomous Control for Safe Driving of Ground Vehicles, Vol. 8, 2010, No. 2/3/4, p. 85-105.
5. BURGIO, G, ZEGELAAR, P. Integrated Vehicle Control Using Steering and Brakes. International Journal of Control, Vol. 79, 2006, No. 2, 162-169.
6. DI CAIRANO, S, TSENG, H. E, BERNARDINI, D, BEMPORAD, A. Vehicle Yaw Stability Control by Coordinated Active Front Steering and Differential Braking in the Tire Sideslip Angles Domain. IEEE Transactions on Control Systems Technology, Vol. 21, No. 4, 2013, p. 1236-1248.
7. EARL Beal, C, CHRISTIAN GERDES, J. Model Predictive Control for Vehicle Stabilization at the Limits of Handling. IEEE Transactions on Control Systems Technology, Vol. 21, 2013, No. 4, p. 1258-1269.
8. HEYDINGER, G. J, GARROTT, W. R, CHRSTOS, J. P, GUENTHER, D. A. Methodology for validating vehicle dynamics simulations. SAE, Paper 900128, 1990.
9. KARBALAEI, R, KAZEMI, G. R, TABATABAEI, S. H. Design of an Integrated AFS/DYC based on fuzzy logic control. IEEE International Conference on Volume Vehicular Electronics and Safety, 2007, p. 1-6.
10. MALAN, S, BORODANI, P, GORTAN, L. Robust performance design for a car steering device. Proceedings of the 33rd IEEE Conference on Decision and Control, 1994, p. 474-479.
11. REN, H, CHEN, S, LIU, G, ZHENG, K. Vehicle State Information Estimation with the Unscented Kalman Filter. Advances in Mechanical Engineering, Vol. 2014, 2014, p. 11-20.
12. YACINE, Z, ICHALAL, D, AIT-OUFROUKH, N, MAMMAR, S, DJENNOUNE, S. Takagi-Sugeno Observers: Experimental Application for Vehicle Lateral Dynamics Estimation. IEEE Transactions on Control Systems Technology, Vol. 23, 2015, No. 2, p. 754-760.
13. ZAKARIA, M, DWIJOTOMO, A, AZMAN, M, TAMALDIN, N. Development Motor Control Unit for Electronic Steering System Test Rig. 2014 IEEE 10th International Colloquium on Signal Processing and its Applications (CSPA), 2014, p. 42-47.
14. ZHAO, L, LIU, Z. Vehicle State Estimation with Friction Adaptation for Four-Wheel Independent Drive Electric Vehicle. Proceeding of the 11th World Congress on intelligent Control and Automation, 2014, p. 4527-4531.