Se propone el diseño en hardware y aplicación de una plataforma de bajo costo para el entendimiento de las dinámicas y variables físicas del tractor, esto permite que las y los estudiantes analicen el comportamiento de algoritmos de control propuestos, en tiempo real por retroalimentación de estados, para la autonomía del vehículo agrícola, utilizando sensores comerciales e interaccionando con Arduino uno o DAQ 6009 de National Instruments utilizadas en las universidades. También se aplica una app de diseño propio para el monitoreo en tiempo real de esta plataforma en sus señales autónomas de control, del sistema de referencia local y de las variables físicas y dinámicas en el tractor, como una alternativa de aprendizaje en línea (laboratorio móvil) para el nivel de Educación Superior. Los resultados obtenidos se comparan con Matlab, y Scilab, para determinar la similitud con estas dos plataformas comerciales y establecer una herramienta alternativa innovadora de autoaprendizaje.

Palabras clave: autonomía, Arduino, DAQ, retroalimentación de estados.

It´s proposethe hardware design and application of a low-cost platform for understanding the dynamics and physical variables of the tractor, this allows students to analyze the behavior of proposed control algorithms, in real time by feedback of states, for the autonomy of the agricultural vehicle, using commercial sensors and interacting with Arduino uno or DAQ 6009 from National Instruments used in universities. An app of its own design is also applied for real-time monitoring of this platform in its autonomous control signals, of the local reference system and of the physical and dynamic variables in the tractor, as an online learning alternative (mobile laboratory ) for the Higher Education level. The results obtained are compared with Matlab, and Scilab, to determine the similarity with these two commercial platforms and establish an innovative alternative self-learning tool.

Keywords: autonomy, Arduino, DAQ, state feedback.

En la actualidad la utilización de los vehículos en diferentes actividades como el transporte de personas, aplicaciones industriales, de rescate, entre otros, están siendo diseñados con una visión de tecnologías de combustión mecánica, híbrida o eléctrica. A partir de estas necesidades en el área automotriz, las y los ingenieros realizan investigación en el diseño de nuevos dispositivos electrónicos para el control del automóvil. Esto es debido al mejoramiento de la electrónica y al avance en la tecnología, que permite desarrollar nuevos sistemas de control que evitan cualquier restricción desde el punto de vista tecnológico. Estos dispositivos, denominados controladores u observadores, que pueden ser implementados en microcontroladores, FPGAs (arreglo de compuertas programables en campo), MEMS (sistemas microelectromecánicos), entre otros, modifican las dinámicas de los vehículos imponiendo fuerzas o momentos de diferentes maneras^{1,2,3,4,5,6,7} y pueden también utilizar sensores que permiten mediciones precisas de las variables que se desean medir, haciendo una alta eficiencia en la acción que el controlador esté realizando, así contribuye a la estabilidad del vehículo, la seguridad y confort.

Sin embargo, hoy en día una de las áreas importantes para el ser humano es la agricultura, que contribuye con la generación de alimentos, en sus diferentes técnicas de cultivo y para ello es importante la utilización de vehículos agrícolas en diferentes labores en la agroindustria^8,9,10,11,12.

Existen trabajos previos en los estudios de las dinámicas y variables del tractor, por ejemplo Eaton (2008) diseña un control autónomo por modos de deslizamiento para maquinaria agrícola, la cual realiza adquisición de datos y tareas de precisión en agricultura¹³. En Zang (2010) establece un sistema de experimentos en realidad virtual (VR) en pruebas para diferentes condiciones de trabajo de rueda, terreno y rueda sobre terreno deslizante¹⁴. Kayacan (2013) realiza el control de las dinámicas yaw (viraje o sobreviraje) y del ángulo de maniobrabilidad para autonomía, monitoreando sus respuestas en el dominio de la frecuencia con un sistema PXI de LabVIEW en un tractor Case New Holland¹⁵. Por otra parte Kim (2014) desarrolla una plataforma para seguridad de operación en tráfico con un simulador de manejo de dos grados de libertad¹⁶. Además Ochoa-Lleras (2016), propone un simulador de pruebas de estabilidad considerando los ángulos de bancada y roll por medio de una plataforma física¹⁷. Sun (2018) realiza la simulación en software de un vehículo agrícola con una estructura protectora de rodamiento en roll, para determinar algunas dinámicas que resultan en cierta colisión al impactarse con una pendiente en forma de banco y colina uniforme, utilizando datos de coeficiente de fricción en piso seco y con detergente inundado¹⁸. Para Hang en 2013, realiza un algoritmo de seguimiento auto guiado para la rastra del tractor con un sensor RTK-GPS¹⁹ y en 2019 propone un simulador para diseño de algoritmos autónomos en operaciones de la rastra con pruebas X, R, C²⁰. Alipour (2019) analiza el modelo matemático de un robot movible con ruedas llamado Tractor-Trailer considerando el deslizamiento longitudinal y lateral de las llantas, además de la propuesta de un control robusto dinámico basado en un algoritmo de modo deslizante para resolver el problema del seguimiento de una trayectoria, verificando sus dinámicas con la simulación en el software multicuerpo ADAMS y Matlab²¹.

Además también existen algunas otras plataformas de aprendizaje en el área comercial como es De Lorenzo, para el entendimiento de sistemas eléctricos, de gasolina, diésel, tanto para el tracto camión y automóvil de combustión y eléctrico, pero cada kit de aprendizaje tiene un costo de cerca de 10,000 USD, sin considerar que no tienen ninguna plataforma para el estudio del tractor²². En la parte de entrenadores de plataforma Hil (Hardware-in-the-Loop), se encuentran algunas compañías de desarrollo de software y hardware, con varios módulos para adquisición de señales como es National Instruments, pero al considerarlos en forma completa tienen un alto costo²³.

Por lo tanto, al considerar la información anterior, que expone resultados en la parte de simulación y aplicación con conceptos entendidos desde la física del vehículo agrícola, resulta la necesidad de entender las dinámicas y variables desde los conceptos simples que corresponden al modelado matemático del tractor, hasta poder entender como introducir la matemática a la electrónica en forma práctica, para el entendimiento de cualquier estudiante de nivel ingeniería²⁴, contribuyendo entonces con la propuesta de una plataforma de aprendizaje en el diseño de tarjetas electrónicas, que se realizan en forma manual con electrónica básica para la medición y estimación de parámetros físicos aplicados al tractor, mediante la utilización de un software como el Proteus, conocido por estudiantes universitarios, obteniendo con esto grandes aplicaciones a niveles de educación y agro-industria.

En este artículo de investigación se plantea estudiar la implementación de dinámicas, variables y algoritmos de control del vehículo agrícola²⁵, obtenidos mediante una plataforma propia con normas internacionales ISO 7401/2011, la cual se conecta a un actuador eléctrico (motor) de asistencia acoplado a la barra de dirección del volante manual para la autonomía del vehículo, lográndolo por medio de la activación del motor eléctrico y por un sistema de referencia propio o control remoto, observando con ello si son correctos los algoritmos controlados, para después implementarlos al tractor en actividades como el riego, rastra o corte de maleza en invernaderos de arándano, frambuesa o zarzamora, ahorrándose tiempo y dinero al realizar pruebas de diagnóstico rápida en la plataforma propia de aprendizaje de dinámicas y variables del vehículo(PPADV), además de comparar los resultados con otras dos plataformas las cuales son Matlab-Simulink y Scilab.

A continuación, se describe un breve marco conceptual sobre el que se basa esta propuesta de la PPADV.

Realizar una plataforma PPADV para que las y los estudiantes y profesionistas del área automotriz puedan aprender a realizar autonomía vehicular a bajo costo y con diseños propios en electrónica.

Existen plataformas para el aprendizaje de dinámicas y variables físicas del vehículo con un costo elevado o sistemas de autonomía vehicular de diferentes compañías automotrices, sin la experiencia de transmitir el conocimiento de la electrónica y el control a bajo costo y sin acceso universal al conocimiento.

Por lo tanto después de entender el objetivo y planteamiento del problema anterior se propone la realización del sistema de aprendizaje de las dinámicas y variables de la plataforma del vehículo autónomo, donde se puede observar en el esquema a bloques de la Figura 1.

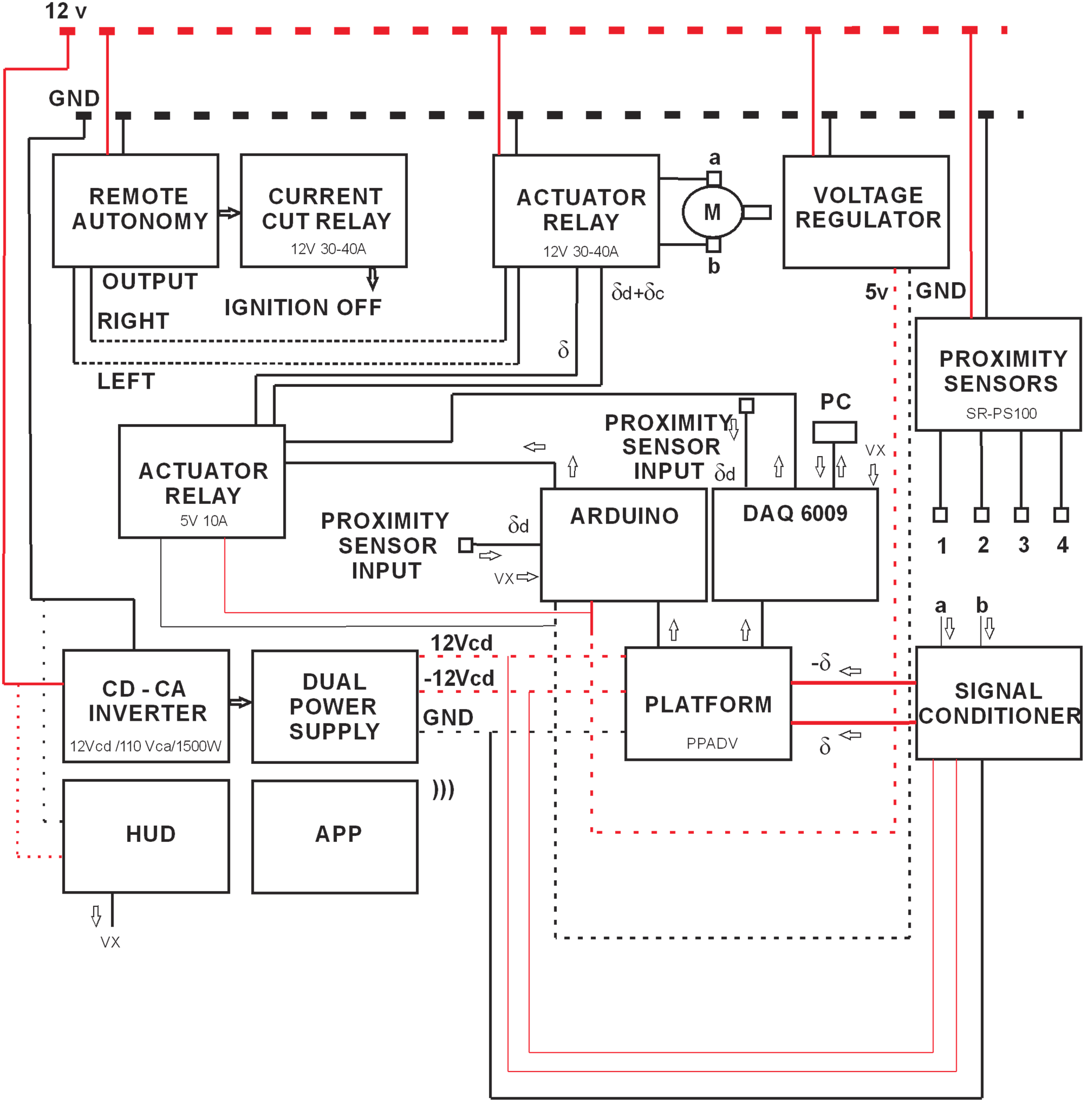
Figura 1. Sistema de plataforma en el aprendizaje de dinámicas y variables del vehículo (SPADV). Fuente: elaboración propia

Configuración del sistema

Se comienza con el módulo de autonomía remota, el cual realiza por control remoto la activación del motor (M) de CD directa (actuador) que se encuentra acoplado al sistema de la barra de volante del tractor John Deere, manejando con esto los ángulos de giro de rueda frontal, además de tener la posibilidad de poder apagar la ignición para el motor de combustión del vehículo agrícola o en el futuro del tractor eléctrico vía señal de radiofrecuencia, esto para la seguridad de las personas que se encuentran en el área de experimentación al momento de estar utilizando la PPADV para configurar los controles activos autónomos automotrices. Los cortes de corriente de ignición y la activación del actuador eléctrico (M) utilizan un relevador de 12 volts (V) a 30 o 40 Amperes (A) de cinco puntas tipo Ford.

Continuando con el sistema de plataforma en el aprendizaje de dinámicas y variables del vehículo (SPADV), existe un inversor de voltaje de 12 Vcd a 110 Vca de 1500 W (para implementarlo en el tractor real) conectado a una fuente dual de +12V/-12V/3A, alimentando a la PPADV que recibe las señales del acondicionador con entradas a, b, de las terminales del motor eléctrico (M), este genera las señales de entrada: δ,-δ (con Norma Internacional ISO 7401/2011) a la plataforma PPADV, produciendo dinámicas y variables del vehículo que se envían a una tarjeta Arduino de bajo costo o una DAQ 6009, donde se programan los algoritmos de control autónomos conectados a relevadores de 5V-10A y 12V a 30 o 40 A, para activar al actuador eléctrico (M), que realiza la tarea de autonomía. Además, mediante una computadora personal (PC) conectada a la tarjeta de adquisición de datos 6009, se observan las dinámicas y variables del vehículo en forma gráfica, así como las señales del sistema de referencia utilizado y la entrada de control autónomo (δ_d+δ_c) al motor eléctrico (M). También la señal de control (δ) al motor (M) y algunos otros parámetros de entrada al Arduino se pueden ver con algún equipo de bajo costo como un osciloscopio, un escáner automotriz o la app libre para análisis de la PPADV en tiempo real para cualquier usuario desarrollada por nosotros, además de tener la posibilidad en esta plataforma PPADV de contar con equipos de bajo precio (sin DAQ 6009 e inversor de 12vcd/110vca/1500w), para un aprendizaje sin demasiados recursos económicos o la plataforma completa (ver la Figura 1) que realiza el diagnóstico de las variables y dinámicas del vehículo agrícola con opciones de aplicación en aula escolar como en laboratorio académico, taller de servicio e implementación física en la agricultura en invernaderos.

Cabe mencionar que el módulo de sensores (1, 2, 3, 4) de proximidad SR-PS100 (spider/distancia de medición 0 m a 2 m) ofrece la variable medida (δ_d) para que cada uno de los subsistemas de la PPADV del vehículo agrícola puedan obtener las diferentes variables y dinámicas del tractor necesarias en los controles activos autónomos. Se agrega que a esta SPADV también se le pueden conectar algunos sensores que miden la velocidad longitudinal (v_x), como puede ser un Head-up Display, que utilice un sensor de efecto Hall (por ejemplo, el modelo 233HUDS-F de la compañía HMC) o el equipo X90 Smart GPS Slope Meter de la compañía AUTOOL con envío de la señal de velocidad longitudinal por GPS, para ser procesada por el Arduino, DAQ6009 o cualquier otra tarjeta electrónica.

El modelo matemático del vehículo agrícola se puede establecer como un cuerpo rígido moviéndose en un espacio libre, de dos o tres grados de libertad, conectado con una superficie terrestre plana a través de las llantas, por ejemplo, en lugares como invernaderos. Además, al considerar las dinámicas estimadas lineales y no lineales del tractor, estas se pueden analizar de forma simplificada con el llamado modelo de la bicicleta^{25, 26}, dando como resultado el poder proponer una variable medida (δ_d) y el siguiente modelado matemático (ver Figura 2).

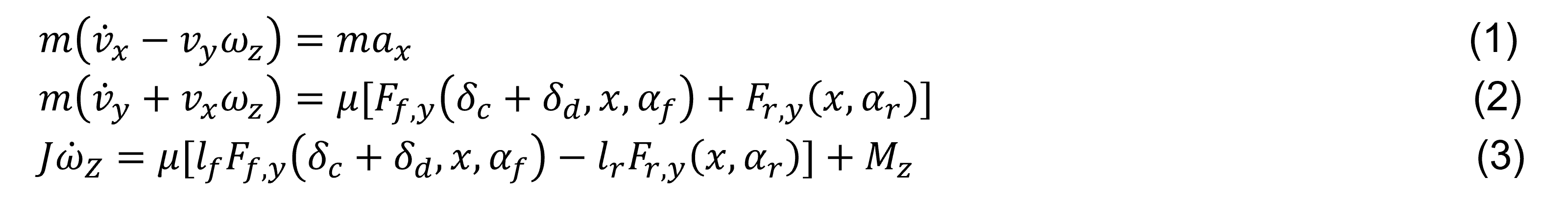
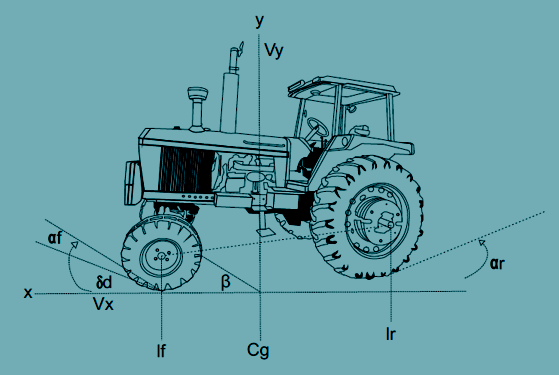
Figura 2. Modelo de la bicicleta utilizado para el vehículo agrícola. Fuente: elaboración propia.

Donde:

m: masa del vehículo [kg],
J: momento de inercia del vehículo [ kg m² ],
l_f,l_r: longitud desde el centro del vehículo hacía la llanta frontal y trasera [m],
v_x: velocidad longitudinal (eje x) del vehículo [m/s],
v_y:, velocidad lateral (eje y) del vehículo [m/s],
x=[v_y,v_x ]: vector compacto del estado del vehículo,
ω_z≅δ ̇_dR: velocidad angular de viraje, la cual está en sincronía con δ_d^27,28;
R: una ganancia constante,
α_f,α_r: :ángulo deslizamiento lateral frontal y trasero [rad],
δ_c,δ_d: componente del ángulo de la llanta impuesto por el controlador y la autonomía respectivamente [rad],
δ ̇_d: la derivada del ángulo impuesto por el volante autónomo (velocidad angular del actuador) [rad],
M_z: Momento de viraje resultado de los frenos activos [N m],
μ: coeficiente de fricción entre suelo y el neumático,

las fuerzas laterales F_f,y,F_r,y (eje y) son funciones del ángulo impuesto a las llantas frontales (δ=δ_d+δ_c), y los ángulos de deslizamiento lateral de las llantas definidos de la siguiente manera:

Para este problema de retroalimentación de estados, se establecerán las entradas de control δ_c y M_z.

Para el problema de control, se reescriben las ecuaciones (2) y (3) de la planta en forma de espacio de estados, se obtiene la velocidad lateral y angular que determinan al controlador lineal de esta propuesta de investigación;

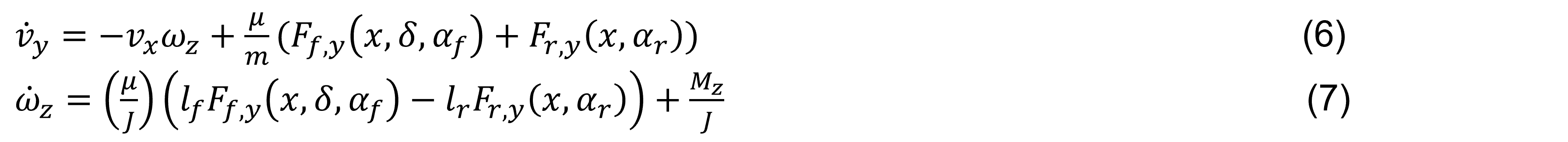
La aceleración lateral a_y puede ser expresada usando la segunda ley de Newton en términos de las fuerzas del neumático lateral:

La fuerza lateral puede ser definida utilizando la conocida fórmula mágica de Pacejka, para sistemas lineales²⁶

Con j=f,r. Las constantes B_j,y, C_j,y, D_j,y en (2) y (3) son determinadas de manera experimental, las cuales se obtienen a partir de las características técnicas del tractor John Deere Modelo 4430 (ver Tabla 1).

Tabla 1: Parámetros reales usados en la simulación del vehículo. Fuente: elaboración propia.

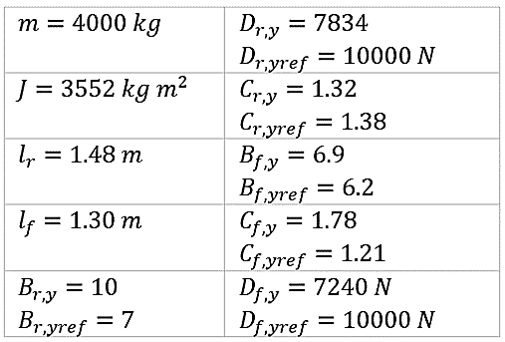
En este artículo se considerará a la aceleración longitudinal a_x casi cero. Además, las fuerzas laterales frontales y traseras de las llantas se pueden analizar de esta otra forma considerando los coeficientes; C_f=D_f,y ∙ C_f,y ∙ B_f,y y C_r = D_r,y ∙ C_r,y ∙ B_r,y, para obtener: F_f,y = C_f α_f y F_r,y = C_r α_r.

El objetivo principal del control es que la salida del sistema x=[v_y, ω_z ] siga asintóticamente un sistema de referencia x_,ref = [vy_,ref, ω_z,ref], el cual tiene como principal característica que sus derivadas son acotadas. De manera más precisa, el generador de referencia es una copia de la planta a controlar en ecuación (6) y (7) despejadas anteriormente;

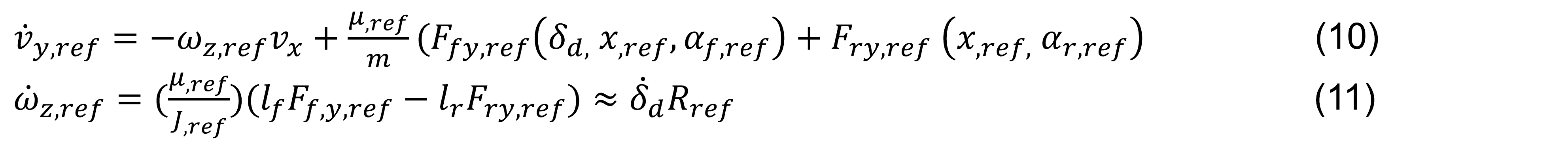
J_,ref=J, μ_,ref = μ=0.9, R_ref > 0, son parámetros apropiados y F_f,y,ref, F_ry,ref que son curvas ideales dependiendo de:

En esta sección se diseña el control de linealización por retroalimentación de estados, el cual utiliza el comportamiento para las dinámicas de las velocidades lateral y de viraje; esto se realizará imponiendo la señal de referencia (10), y (11), a través de la implementación de las entradas de control δ_c y M_z.

Considerando las ecuaciones en (6) y (7), el sistema de la planta con sus fuerzas laterales frontales y traseras (F_f,y= C_f α_f y F_r,y = C_r α_r.) se pueden analizar de esta forma:

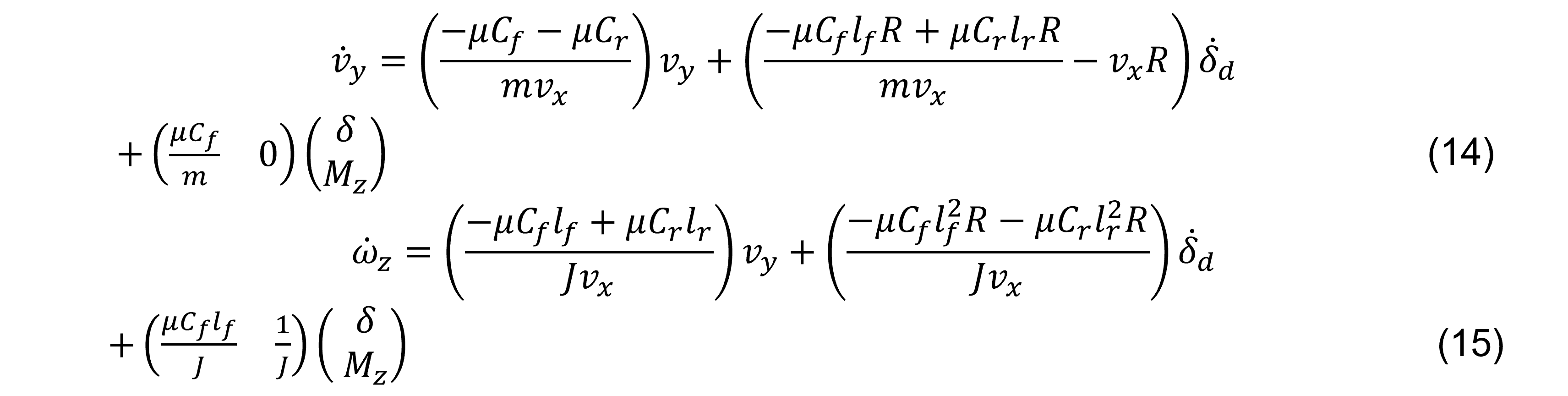
Para las ecuaciones (10) y (11), se toma en cuenta a las fuerzas laterales frontales y traseras, con los siguientes coeficientes; C_f,ref = D_f,yref ∙ C_f,yref ∙ B_f,yref y C_r,ref = D_r,yref ∙ C_r,yref ∙ B_r,yref, para obtener F_fy,ref = C_f,ref α_f,ref y F_ry,ref = C_r,ref α_r,ref. Donde; C_f,ref ≠ C_f y C_r,ref ≠ C_r. (Ver Tabla 1). Por lo tanto, se obtiene el sistema de referencia que se representa en forma matricial para mejor entendimiento al momento de analizarlo en hardware y software:

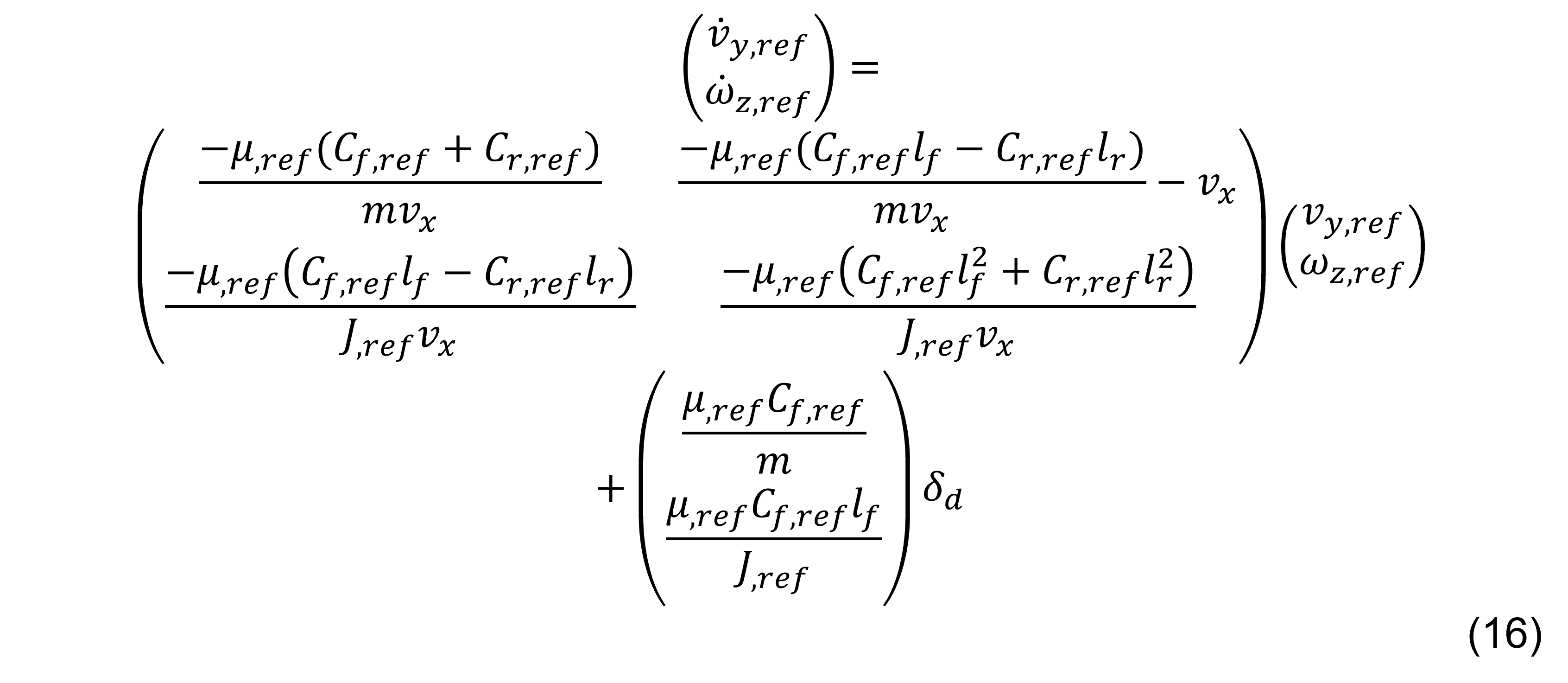
Considerando los errores para la velocidad lateral y angular de viraje de esta manera;

y los errores dinámicos se establecen mediante;

Lo siguiente son los requerimientos para la ley de control estableciendo una función candidata de Lyapunov²⁵;

Considerando a la ecuación (21) positiva para mostrar que es continuamente decreciente a lo largo de cualquier trayectoria y su derivada negativa, asegurando que el sistema tenga estabilidad asintótica como se demuestra a continuación;

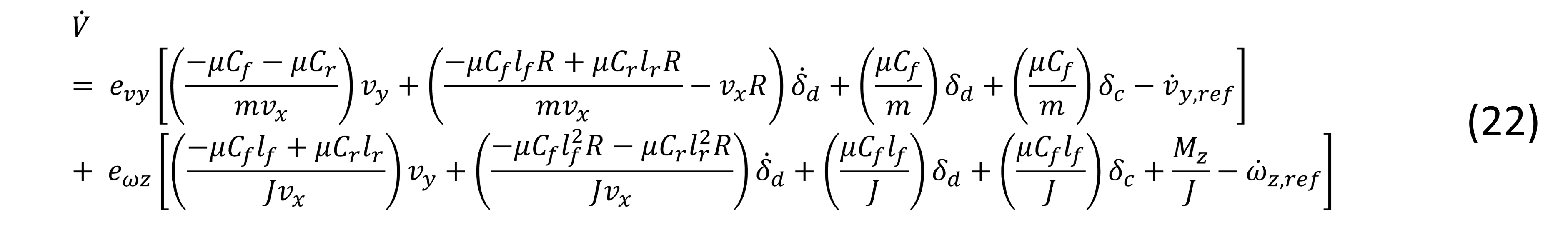
Además cada término de la ecuación (22) se iguala a las ganancias multiplicadas por el error, para establecer que la derivada de la función de Lyapunov sea menor a cero;

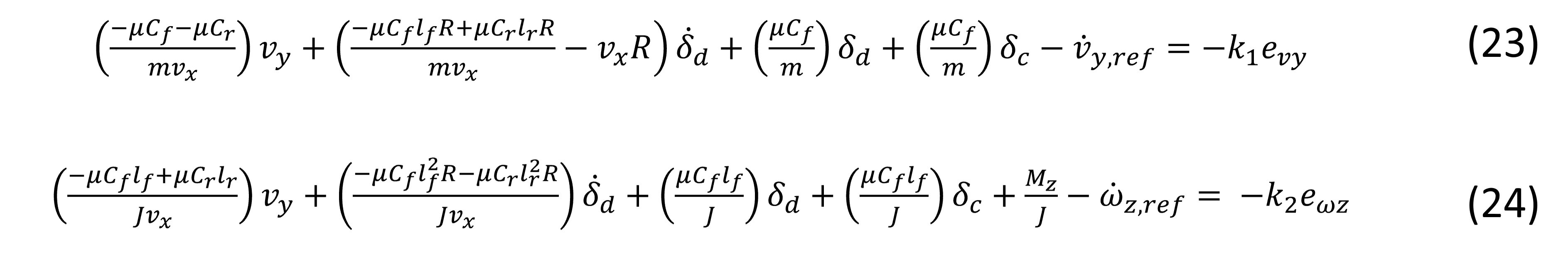
Por lo tanto, de las ecuaciones (23) y (24), se obtienen las entradas de control despejando los términos δ_c y M_z;

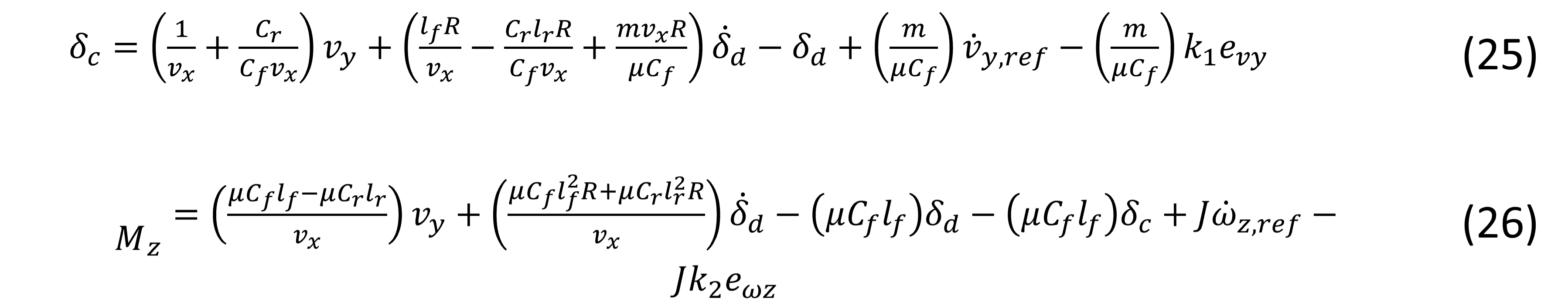
Donde k_i > 0,i = 1,2, y las entradas de control en (25) y (26), serán impuestas en (22), comprobándose la estabilidad del sistema:

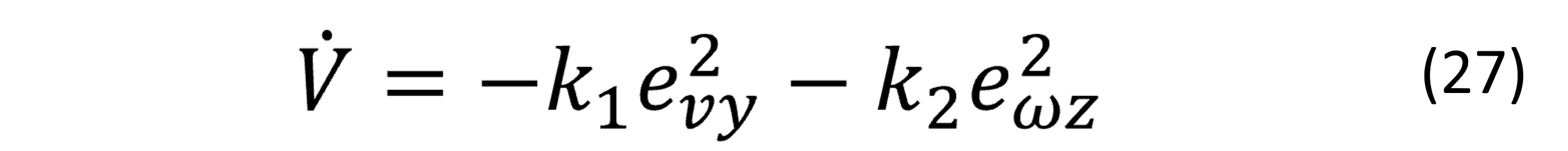
Además de reescribir la derivada de la función de Lyapunov en (27), de la siguiente manera;

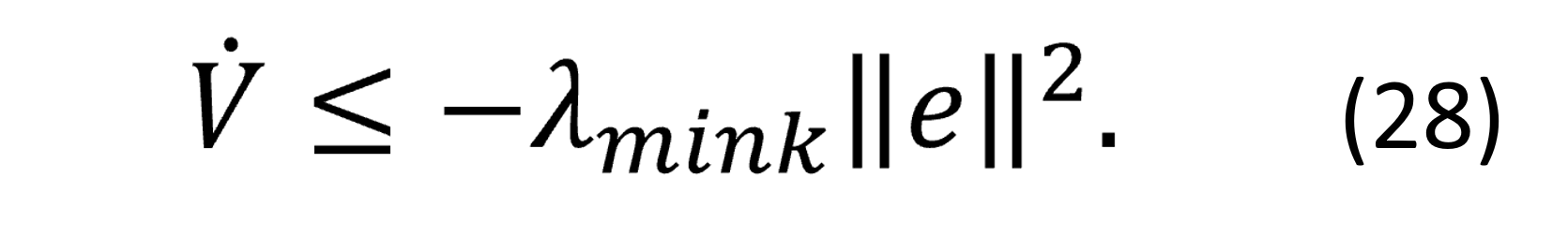
Estableciendo una λ_mink > 0, que representa una ganancia mínima igual para k₁, k₂ y considerando e=(e_vy,e_wz).

Para la implementación de las dinámicas, variables y controlador en el tractor, se realiza una conexión de los sensores de proximidad (δ_d), que generan señales estimadas, como la velocidad lateral, v_y, y angular de viraje, w_z, ángulos de deslizamiento de las ruedas frontales del tractor, α_f, y las señales de control δ_c, M_z que se comparan con el sistema de referencia (v_y,ref, ω_z,ref, α_f,ref, α_r,ref, F_f,y,ref, F_ry,ref) para la aplicación al tractor o para el ajuste del modelo matemático en la plataforma PPADV. Esta metodología se puede ver en Figura 3, que describe un método experimental con el enfoque de una investigación práctica, mediante la técnica de teorías de control y el uso de hardware (diseños propios) y software para la recolección de datos en computadora, tableta o celular.

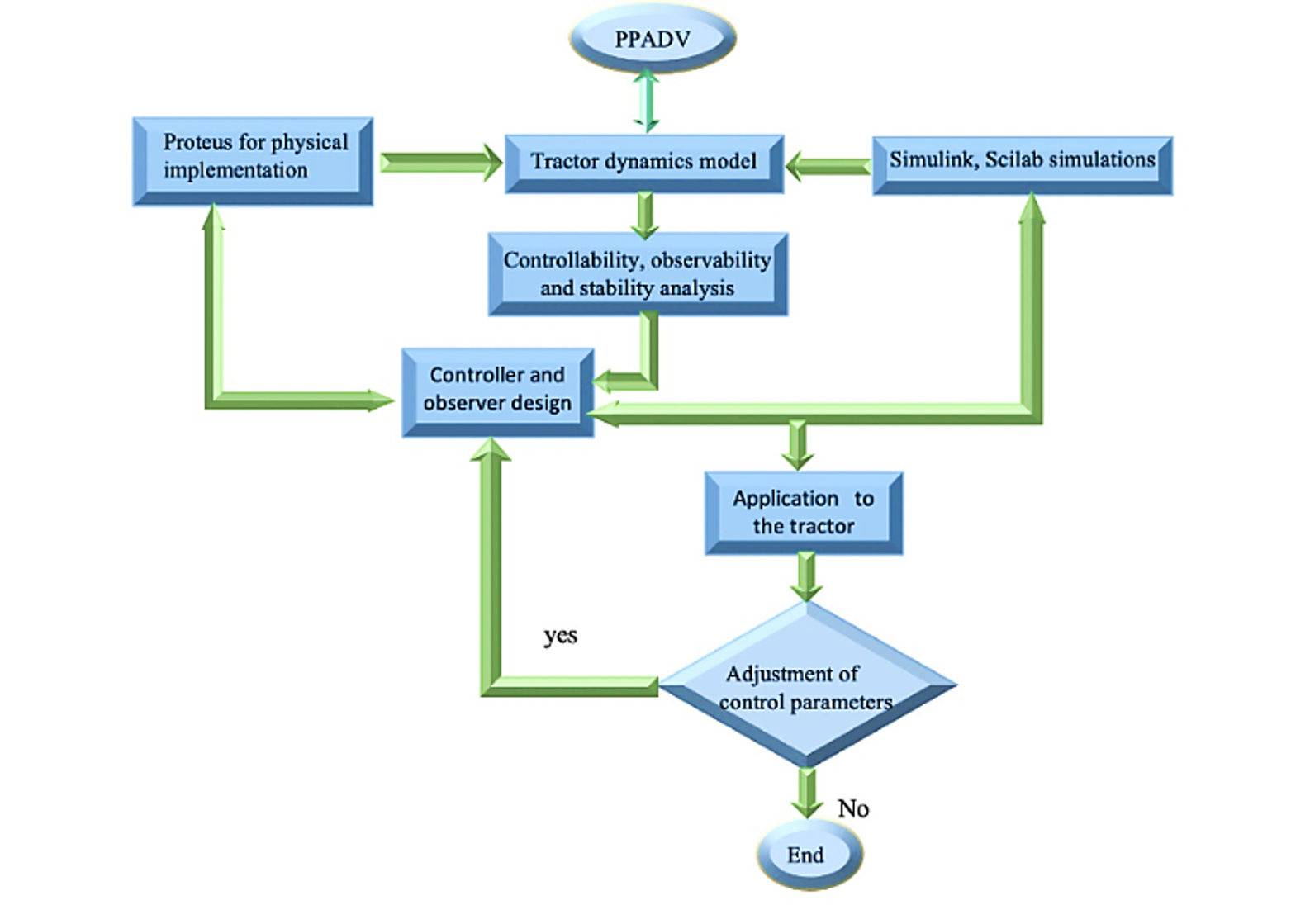
Figura 3. Lógica de operación PPADV. Fuente: elaboración propia

En los ajustes de los modelos matemáticos se utilizan algunos softwares tradicionales como el Matlab-Simulink o Scilab, para el diseño de la planta y su controlador, pero en la implementación física de la PPADV se conecta un Arduino uno para establecer el control autónomo en su programación con un IDE (entorno de desarrollo integrado), cuando se desea obtener una plataforma de bajo costo, como se puede ver en la siguiente programación:

void loop() {
sensorValueA0 = analogRead(sensorA0); // realizar la lectura
sensorValueA1 = analogRead(sensorA1); // realizar la lectura
sensorValueA2 = analogRead(sensorA2); // realizar la lectura
sensorValueA3 = analogRead(sensorA3); // realizar la lectura
jd=sensorValueA0/204.8;// Convercion de valor analogico a Voltaje
//wz2=sensorValueWz/204.8;
//alfaf2=sensorValuealfaf/204.8;
//vx=map(sensorValueVx, 0, 1024, 0, 90);
//formulas algoritmicas
Wz=jd*R; //formula Algoritmica Wz
Vy=(Wz)*(-0.97); //formula Algoritmica Vy
AlfaF=1 +(-lf_vx*Wz)-(Vy*0.5); //formula Algoritmica Alfa F
AlfaR= -(Vy*0.5)+(-lf_vx*Wz); //formula Algoritmica Alfa R
fFy= AlfaF*(-0.93); //formula Algoritmica f Fy
fRy= AlfaR*(-0.998); //formula Algoritmica f Ry
Wzref=Wz;
Vyref=Wzref*(-1.04); //formula Algoritmica Vyref
AlfaFref=1 +(-lf_vx*Wzref)-(Vyref*0.5); //formula Algoritmica Alfa F Ref
AlfaRref= -(Vyref*0.5)+(-lf_vx*Wzref); //formula Algoritmica Alfa R ref
fFyref= AlfaFref*(-0.83); //formula Algoritmica f Fy ref
fRyref= AlfaRref*(-1.13); //formula Algoritmica f Ry ref
EWz=Wz-Wzref; //formula Algoritmica Error Wz
EVy=Vy-Vyref; //formula Algoritmica Error Vy
DerVyref= -Wzref*Vx+(0.00058)*(fFyref+fRyref); //formula Algoritmica DerVyref
DeltaC=(-0.5)*Vy+(-0.1)*Wz+constantejd+(0.019367*DerVyref)+EVy; //formula Algoritmica DeltaC
DerWzref=(0.0002533)*((2*fFyref)-(2*fRyref))*(-1); //formula Algoritmica DerWzref
//DerWzref=(0.0002533)*((2*0.79)-(2*2.15))*(-1);
Mz=(0.435)*Vy+(0.57*Wz)+(-(-0.97))*constantejd+(-(-0.8))*DeltaC+1*DerWzref-EWz;//formula Algoritmica Mz

O una tarjeta DAQ 6009 NI/USB programada en LabVIEW con opciones de software en íconos virtuales a un costo mayor, pero también aplicable con la PPADV, como se establece en la Figura 4.

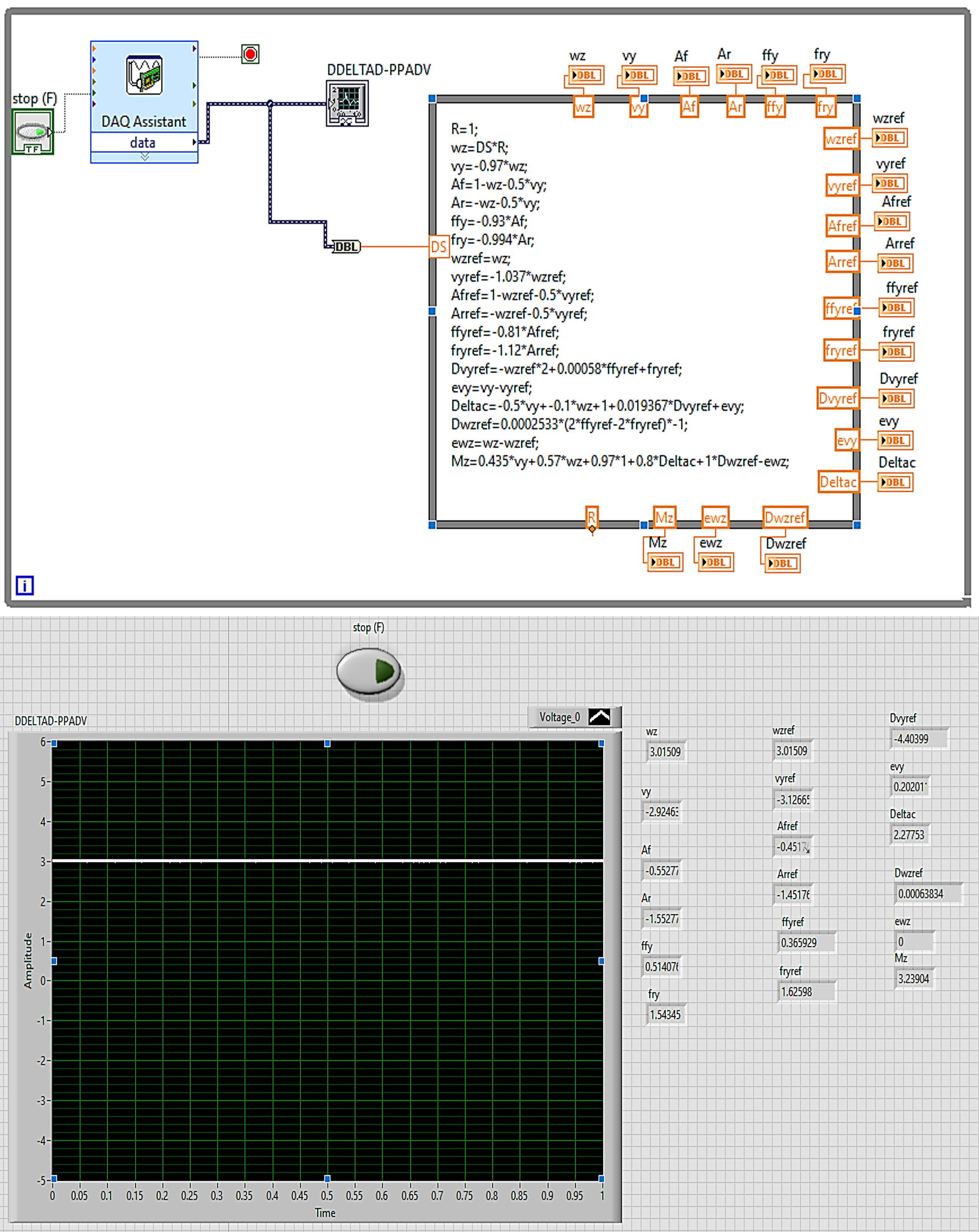
Figura 4. Diseño de modelos matemáticos para vehículo agrícola con plataforma PPADV utilizando DAQ 6009 NI/USB²³

En la parte de resultados se observa el diseño del hardware de la plataforma propia de aprendizaje de dinámicas y variables para la autonomía del vehículo agrícola, así como el diseño en 3D y la forma de fabricación con software Proteus o con tarjetas comerciales, verificándose dicha información en el Apéndice de desarrollo de control, de autoría propia.

Para la parte experimental de la plataforma PPADV, es necesario implementarla en los campos de cultivo como una aplicación real, donde se establecerán las conexiones y la programación para el análisis y aprendizaje de las dinámicas del vehículo agrícola. Como una primera actividad, se debe realizar la implementación del actuador en el volante del tractor John Deere, como se muestra en la Figura 5.

Figura 5. Implementación mecánica con motor de CD, al volante para control de autonomía. Fuente: elaboración propia

Enseguida se continúa con la conexión de la plataforma PPADV en el vehículo agrícola, conjuntamente con todo el sistema SPADV, para el análisis de dinámicas y variables del tractor en tiempo real, como se muestra en la Figura 6.

Figura 6. a) Plataforma PPADV instalada en tractor John Deere. Fuente: elaboración propia; b) App para análisis de dinámicas en tiempo real para cualquier usuario. Fuente: elaboración propia

También se realiza la implementación de la PPADV, la cual interacciona con la tarjeta Arduino uno o DAQ 6008/6009 NI USB mediante su programación en computadora, para que reciba las dinámicas y variables del tractor y programar la teoría de control propuesta en este artículo de investigación (ver Figura 7).

Figura 7. Programación de la plataforma PPADV. Fuente: elaboración propia

Por último, se muestran los resultados de las dinámicas y variables de la PPADV, comparadas con los simuladores de Scilab, Matlab-Simulink y LabVIEW de National Instruments, además de salidas de Arduino uno (ver las figuras 8 y 9).

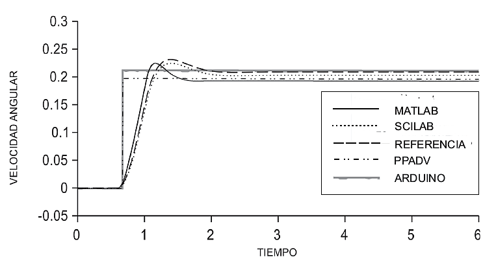
Figura 8. Velocidad angular ω_z. (Software-simulaciones)

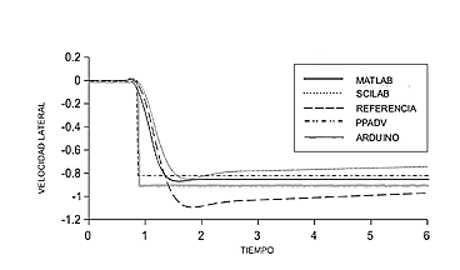
Figura 9. Velocidad lateral v_y. (Software-simulaciones)

En el desarrollo de este artículo de investigación se determinó la propuesta de un monitoreo de variables y dinámicas aplicadas al vehículo agrícola, entendiendo que al utilizar una plataforma de bajo costo se puede aprender cómo funciona la física del tractor para estudiantes o profesionistas, midiendo las señales mediante una aplicación (app) libre que utiliza la relación de unidades físicas con respecto a voltaje, a entender la diferencia de resultados al comparar la PPADV con otras plataformas comerciales, además de establecer los valores de voltaje en la Tabla 1 (ANEXO G), localizada en el Apéndice de desarrollo de control, de los cuales se concluye que la implementación en campo de la PPADV en ω_z trabaja adecuadamente, porque estos resultados permiten manejar el control activo para la autonomía del tractor en forma eficiente o en vehículos utilitarios con acotación en la parte de movimiento lineal.

Los autores agradecen a los campesinos de parcelas de la Zona Sur de Jalisco, que facilitaron esta investigación.

1. ACOSTA-LÚA, C., Di Gennaro, S., Sánchez-Morales, M. U, An Adaptive Controller Applied to an Anti–lock Braking System Laboratory. DYNA [en línea]. Medellín, Colombia: Universidad Nacional de Colombia, 83, (199), 69-77. 2016. [Fecha de consulta: 01 de enero de 2022]. ISSN:0012-7353. DOI: http://dx.doi.org/10.15446/dyna.v83n199.51831 ISSN: 0012–7353.
2. ALIGIA, Diego, A., Magallan, Guillermo, A., De Angelo, Cristian, H, 2018. Control de Tracción para un Vehículo Eléctrico basado en Observadores no Lineales. Revista Iberoamericana de Automática e informática Industrial [en línea]. Valencia, España: CEA, 1 (15), 112–123. 2019. [Fecha de consulta: 09 de enero de 2022]. DOI: https://doi.org/10.4995/riai.2017.8736 ISSN: 1697-7920.
3. MANSOUR, Ataei; Amir, Khajepour y Soo, Jeon. Model Predictive Control for integrated lateral stability, traction/braking control, and rollover prevention of electric vehicles. International Journal of Vehicle Mechanics and Mobility [En línea]. United Kingdom: Vehicle System Dynamics, 1 (58), 49-73. 2019. [Fecha de consulta: 15 de enero de 2022]. DOI:10.1080/00423114.2019.1585557. https://doi.org/10.1080/00423114.2019.1585557 ISSN-L: 0042-3114
4. BELTRÁN, Alberto, et al. Simulación y control de la velocidad y par electromagnético de un motor de inducción trifásico: Un enfoque a vehículos eléctricos. Revista Iberoamericana de Automática e informática Industrial [en línea]. Valencia, España: CEA, 16, 308–320. 2019. [Fecha de consulta: 15 de enero de 2022]. DOI: https://doi.org/10.4995/riai.2019.10452 ISSN: 1697-7920.
5. HONGZHOU, Hu y Zhihua, Zhong. 2019. Explicit-Implicit Co-Simulation Techniques for Dynamic Responses of a Passanger Car on Arbitrary Road Surfaces. Engineering [en línea]. China: Engineering Science Press, 5, (6), 1171-1178. 2019. [Fecha de consulta: 17 de enero de 2022]. DOI:10.1016/j.eng.2019.09.003 ISSN: 2095-8099.
6. LIQIN, Sun, et al. Research on Switching Interconnection Modes and Game Control of Interconnected Air Suspension. Energies [en línea]. Switzerland: MDPI, 12 (17), 1-23. 2019. [Fecha de consulta: 20 de enero de 2022]. DOI: https://doi.org/10.3390/en12173218 E-ISSN: 1996-1073.
7. FEN, Lin, et al. Integrated Avoid Collision Control of Autonomous Vehicle Based on Trajectory Re-Planning and V2VInformation Interaction. Sensors [en línea]. Switzerland: MDPI, 20 (4), 1-26. 2020. [Fecha de consulta: 20 de enero de 2022]. DOI: https://doi.org/10.3390/s20041079 ISSN: 1424-8220.
8. REINA, Giulio, et al. Ambient awareness for agricultural robotic vehicles. Special Issue: Robotic Agriculture. Biosystems engineering [en línea]. United Kingdom: Article in Press, 1-19. 2020. [Fecha de consulta: 11 de julio de 2020]. DOI:10.1016/j.biosystemseng.2015.12.010 ISSN: 1537-5129
9. COOK, Joshua T, et al. Dynamics modeling and robotic-assist, leader-follower control of tractor convoys. Journal of Terramechanics, [en línea]. USA: Article in Press, 1-16. 2017. [Fecha de consulta: 12 de julio de 2020]. DOI:10.1016/j.jterra.2017.05.002 ISSN 0022-4898
10. JIA, Chao; Qiao, Wei y Qu, Liyan.. Modeling and Control of Hybrid Electric Vehicles: A case Study for Agricultural Tractors. Conference: 2018 IEEE Vehicle Power and Propulsion Conference (VPPC) [en línea], Chicago, IL, USA: IEEE, 1-6. 2018. [Fecha de consulta: 12 de julio de 2020]. DOI:10.1109/VPPC.2018.8604997. https://ieeexplore.ieee.org/document/8604997 ISSN: 1938-8756
11. NEBOT, Eduardo. Robotics: From Automation to Intelligent Systems. Engineering [en línea], China: Elsevier, 4, 446-448. 201. 2018. [Fecha de consulta: 21 de enero de 2022]. DOI: 10.1016/j.eng.2018.07.018 ISSN: 2095-8099.
12. VAN LOON, Jelle, et al. Scaling agricultural mechanization services in smallholder farming systems: Case studies from sub Saharan Africa, South Asia, and Latin America. Agricultural Systems [en línea], New Zealand: Elsevier, 180, 1-13. 2020. [Fecha de consulta: 21 de enero de 2022]. DOI: 10.1016/j.agsy.2020.102792 ISSN: 0308-521X.
13. EATON, R. et al. Autonomous Farming: Modeling and Control of Agricultural Machinery in a Unified Framework. 15 International conference on Mechatronics and Machine Vision in Practice (M2VIP08) [en línea], Auckland, New-Zealand: IEEEXplore, pp. 499-504. 2008. [Fecha de consulta: 25 de enero de 2022]. DOI: 10.1109/MMVIP.2008.4749583 ISBN:978-1-4244-3779-5
14. ZANG, Yu, et al. Virtual Reality and the Application in Virtual Experiment for Agricultural Equipment. 4th Conference on Computer and Computing Technologies in Agriculture (CCTA) [en línea], Nanchang, China: Springer Link, pp. 257-268. 2010. [Fecha de consulta: 25 de enero de 2022]. https://doi.org/10.1007/978-3-642-18354-6_32
15. KAYACAN, Erkan, et al. Modeling and Identification of the Yaw Dinamics of an Autonomous Tractor. IEEE 2013 9th Asian Control Conference (ASCC) [en línea], Istanbul: IEEEXplore, pp. 1-6. 2013. [Fecha de consulta: 25 de enero de 2022]. DOI:10.1109/ASCC.2013.6606388. https://ieeexplore.ieee.org/document/6606388
16. KIM, Yu-Yong, et al. Development of Driving Simulator for Safety Training of Agricultural Tractor Operators. Journal of Biosystems Engineering [en línea], Korea: The Korean Society for Agricultural Machinery, 39 (4), 389-399. 2014. [Fecha de consulta: 26 de enero de 2022]. https://koreascience.kr/article/JAKO201436438763727.page ISSN: 2234-1862.
17. OCHOA-LLERAS, Nicolas, et al. Development of an Open-Source Tractor Driving Simulator for Tractor Stability Test. Journal of agricultural safety and health [en línea], USA: American Society of Agricultural and Biological Engineers, 22 (4), 227-246 [Consulta: 26 Enero 2022]. DOI: 10.13031/jash.22.11774 ISSN: 1074-7583
18. SUN, Chaoran, et al. Physics engine application to overturning dynamics analysis on banks and uniform slopes for an agricultural tractor with a rollover protective structure. Biosystems Engineering, [en línea], United Kingdom: Elsevier, 185, 150-160. 2019. [Fecha de consulta: 26 de enero de 2022]. https://doi.org/10.1016/j.biosystemseng.2018.06.005 ISSN: 1537-5110
19. HAN, Xiong-Zhe, et al. Development of a Patch Generation and Tracking Algorithm for a Korean Auto-guidance Tillage Tractor. Journal of Biosystems Engineering [en línea], Korea: The Korean Society for Agricultural Machinery, 38 (1), 1-8. 2013. [Fecha de consulta: 27 de enero de 2022]. DOI:10.5307/JBE.2013.38.1.001 ISSN: 2234-1862.
20. HAN, Xiongzhe, et al. Simulation Study to Develop Implement Control and Headland Turning Algorithms for Autonomous Tillage Operations. Journal of Biosystems Engineering [en línea], Korea: The Korean Society for Agricultural Machinery, 44, 245-257. 2019. [Fecha de consulta: 27 de enero de 2022]. DOI:10.1007/s42853-019-00035-9 ISSN: 2234-1862
21. ALIPOUR, Khalil; Babaei-Robat, Arsalan y Tarvirdizadeh, Bahram. Dynamics modeling and sliding mode control of tractor-trailer wheeled mobile robots subject to wheels slip. Mechanism and Machine Theory [en línea], Portugal: Elsevier, 138, 16-37. 2019. [Fecha de consulta: 28 de enero de 2022]. https://doi.org/10.1016/j.mechmachtheory.2019.03.038 ISSN 0094-114X.
22. DE LORENZO, 2020. Engineering Training Solutions. En: Autotronica [en línea]. Disponible en https://www.edylab-equipamientos.com/wp-content/descargas/DE_LORENZO/ELEC-6-AUTOTRONICA.pdf Fecha de consulta: 28 de enero 2020].
23. NATIONAL Instruments, 2020. Plataforma Hil. En: NI [en línea]. Disponible en: https://www.ni.com/es-mx/innovations/automotive/hardware-in-the-loop.html [Fecha de consulta: 29 de enero de 2020].
24. MONZO, Carlos, et al. Lab@Home: The Open University of Catalonia Hands-on Electronics Laboratory for Online Engineering Education. Electronics [en línea], Suiza: MDPI, 9 (2), 1-11. 2020. [Fecha de consulta: 30 de enero de 2020]. https://doi.org/10.3390/electronics9020222 ISSN: 2079-9292
25. RAJAMANI, R, 2011. Vehicle Dynamics and Control. 2a ed. New York: Springer. ISBN 9780387263960
26. PACEJKA, H.B. Tyre and Vehicle Dynamics. 1a ed. Butterworth-Hein: Elsevier. 2005.
27. BENTON-DERRICK, J, Bevly, et al. Adaptive Control of a Farm Tractor with Varying Yaw Dynamics Accounting for Actuator Dynamics and Saturations. 17th IEEE International Conference on Control Applications Part of 2008 IEEE Multi-conference on Systems and Control [en línea], San Antonio, Texas, USA: IEEE Xplore, pp. 547-552. 2008. [Fecha de consulta: 30 de enero de 2022]. DOI: 10.1109/CCA.2008.4629591. https://ieeexplore.ieee.org/document/4629591
28. BORRI, A. et al. Optimal Workload Actuator Balancing and Dynamic Reference Generation in Active Vehicle Control. Journal of the Franklin Institute [en línea], USA: Elsevier, 4, 1722-1740. 2017. [Fecha de consulta: 30 de enero de 2022]. DOI:10.1016/j.jfranklin.2016.12.012 ISSN. 0016-0032