Año 7, Número 2. Enero - Abril, 2020. 
Control estadístico multivariado de procesos basado en análisis de componentes principales para industria automotriz
Multivariate statistical process control based on principal component analysis for the automotive industry
Tecnológico Nacional de México - ITS de Guanajuato / Universidad de Guanajuato
Por: Juana Edith Lozano Hernández, María Guadalupe de Lourdes Acosta Castillo, Jorge Luis Morales Martinez y Luis Armando Torres Pérez / Ver en pantalla completa
Resumen
Este trabajo presenta la implementación del control estadístico multivariado de procesos basado en componentes principales (MSPC-PCA). Se analizaron dos conjuntos de datos con 28 mediciones de cinco características de calidad del proceso de producción de bimetales para termostatos. Los datos se encuentran disponibles en el paquete MSQC del Software R como los conjuntos Bimetal1 y Bimetal2. El análisis se realizó en dos etapas, para cada una se aplicó un análisis de componentes principales (PCA) para reducir la dimensión del problema. Posteriormente, se utilizó la técnica de cartas de control T2 de Hotelling basada en PCA. Al aplicar este análisis, resultó suficiente trabajar con solo dos componentes principales, que representaron más del 80 % de variabilidad. Finalmente, la implementación de las cartas de control T2 de Hotelling, mostró que el proceso en la Fase I estuvo en control, mientras que en la Fase II se detectó un punto fuera del límite de control, indicando la presencia de causas especiales y por lo tanto de un proceso fuera de control.
Palabras clave: Control estadístico multivariado de procesos, Análisis de componentes, Gráficos de control, T2 de Hotelling.
Abstract
This article shows the implementation of multivariate statistical process control based on principal component analysis. The study analyzes two datasets with 28 measurements and five quality characteristics from a bimetal production process for thermostats. All data is available in MSQC package of the Software R as well as the sets Bimetal 1 and Bimetal 2. The analysis was carried out in two stages: Phase I and II. For each one, principal component analysis (PCA) was applied to reduce the dimension of the problem. Subsequently, the control card technique T^2 de Hotelling based on PCA was used. With the application of the PCA, it was sufficient to work with only two main components which represented more than 80% of variability. Finally, the implementation of the control chartT^2 de Hotelling, showed that the process in Phase I was in control, while in Phase II a point outside the control limit was detected. It indicates the presence of special causes and therefore a process out of control.
Keywords: Multivariate statistical process control, Principal component analysis, Control chart, T2 of Hotelling.
Introducción
Con el crecimiento de la industria manufacturera, se ha incrementado la competencia entre las empresas productoras. Además, los clientes se han vuelto cada vez más exigentes con la calidad de los productos que adquieren. A causa de esto, las organizaciones han enfocado sus esfuerzos en el control y mejora de la calidad. Para responder al crecimiento de la demanda, actualmente las empresas del sector industrial han implementado la automatización de los procesos, generando así una producción más acelerada. Por otro lado, para controlar la calidad de los productos es necesario vigilar más de una característica simultáneamente¹.
El control estadístico de procesos (Statistical Process Control, SPC) es una de las herramientas más utilizadas para evaluar el comportamiento de las características de calidad a lo largo del proceso. La técnica de control estadístico de procesos más utilizada es el gráfico de control. Debido a que el SPC se basa en estadísticas univariadas y gráficos de control univariados, en los que solo una variable se monitorea y/o visualiza a la vez2, su implementación para un conjunto de diversas variables podría traer consigo una serie de desventajas, entre ellas:
- El número de gráficos de control a implementar y vigilar puede llegar a ser relativamente grande, esto dependiendo del número de características que se deseen controlar.
- Al realizar el control de las características de manera independiente se está obviando cualquier tipo de relación que pudiera existir entre las características de calidad³.
Por lo tanto, a medida que aumenta el número de variables que se monitorean, el enfoque para visualizar una variable a la vez reduce su rendimiento y es más conveniente utilizar estadísticas y gráficos multivariados², es decir, resulta de mayor utilidad aplicar el Control Estadístico Multivariado de Procesos (Multivariate Statistical Process Control, MSPC). Sin embargo, Kourti y MacGregor, citados por Camacho, Pérez, García y Maciá2 afirman que el MSPC tradicional no tiene en cuenta la correlación entre las variables, lo que puede llevar a problemas de precisión y computación debido al mal acondicionamiento. De esto se concluye que cuando el número de variables es muy grande y/o están altamente interrelacionadas, se recomienda el uso de métodos de variables latentes, como el Análisis de Componentes Principales (Principal Component Analysis, PCA)².
El propósito de este artículo es mostrar una aplicación de control estadístico multivariado de procesos basado en componentes principales para analizar el estado de un proceso de producción de bimetales utilizados en sistemas de refrigeración para la industria automotriz, en el cual se miden cinco características de calidad y se generan 28 muestras. La aplicación se efectuó en dos etapas: Fase I y Fase II. Para cada etapa, se realizó el análisis de componentes principales, y posteriormente se procedió al control estadístico de procesos generando gráficos de control T2 de Hotelling. Para finalizar, y con la intención de complementar el estudio, se determinaron los índices de capacidad del proceso.
Objetivo
Analizar el estado y la capacidad de un proceso de producción de bimetales, mediante la aplicación de control estadístico multivariado de procesos basado en componentes principales.
Planteamiento del problema
Debido al incremento de la competitividad en el sector industrial, ha resultado necesario para las empresas manufactureras conocer constantemente el estado de sus procesos. Más aún, las normas ISO 9001-2015 Sistemas de Gestión de la Calidad-Requisitos⁴ e IATF 16949-2016 Sistemas de Gestión de la Calidad Automotriz⁵ indican como requisito que las empresas lleven a cabo el control de sus procesos. Para realizarlo se recurre a la aplicación de herramientas estadísticas que permitan detectar variaciones y predecir el comportamiento del proceso. Una de las herramientas más utilizadas es el Control Estadístico de Procesos (Statistical Process Control, SPC).
El control estadístico univariado de procesos se enfoca en el estudio del comportamiento del proceso evaluando solo una variable. Sin embargo, durante el desarrollo de un proceso influyen varios factores: mano de obra, maquinaria, material, entre otros, que pueden causar variación en distintas etapas del desarrollo del proceso. Por ello se debe estudiar más de una característica de calidad, es decir, se tendrá que medir más de una variable, añadiendo que dichas variables podrían estar fuertemente interrelacionadas. Al aplicar control estadístico univariado se omite la interrelación entre las variables, y sus efectos. Como consecuencia, se ha incurrido en la necesidad de que los procesos analizados con métodos univariados se analicen con métodos multivariados.
Método de trabajo
A continuación, se presentan los métodos que se utilizaron en este estudio.
Para la Fase I:
- Pruebas de normalidad univariada. Para analizar si los datos se distribuyen normalmente se utilizó como herramienta gráfica el histograma, el cual proporciona información visual para establecer una hipótesis inicial de la distribución de los datos, ya que permite identificar la media, la varianza y la asimetría. Además, es posible detectar la existencia de valores atípicos, los cuales se identificarán en forma de colas largas. Así mismo, las conclusiones generadas a partir de la observación de dichos gráficos se reafirmaron con la implementación de la prueba de normalidad de Jarque- Bera.
- Pruebas de normalidad multivariada. En este caso la herramienta gráfica implementada fue una matriz de dispersión, y para confirmar las conclusiones visuales se aplicó la prueba de Mardia, que es una generalización de la prueba de asimetría y de curtosis univariada y es una de las más populares en la evaluación de la normalidad multivariada.
- Análisis de componentes principales. Se determinó la matriz de proporción de varianza para cada uno de los componentes. Posteriormente se determinaron las componentes que representaran más del 80% de la variabilidad, utilizando el método de porcentaje propuesto por Rencher⁶.
- Gráficos de control multivariado. Determinadas las componentes principales, los gráficos de control multivariado utilizados fueron el elipsoide de confianza y el gráfico de control T2 de Hotelling.
- Índices de capacidad basados en PCA. Para cada una de las componentes, se calcularon los índices de capacidad MCp, MCpk, y MCpm.
Para la Fase II:
- De manera análoga a la Fase I, se aplicaron los cinco métodos anteriores. Sin embargo, cabe destacar que para el caso de los Gráficos de control multivariado, con base en los límites de control obtenidos en la Fase I, se graficaron los datos correspondientes a los componentes generados en esta fase.
Resultados
Se analizaron dos conjuntos de datos con 28 mediciones de cinco características de calidad del proceso de producción de bimetales para termostatos. Los datos se encuentran disponibles en el paquete MSQC del Software R como los conjuntos Bimetal1 y Bimetal2. Dichas características deben cumplir ciertos límites de especificación establecidos por el departamento de Ingeniería de la empresa fabricante de bimetales, los cuales se incluyen en la Tabla 1.
Tabla 1. Especificaciones para las variables.
| Especificaciones de las variables del bimetal | |||||
| Deflexión | Curvatura | Resistividad | Dureza b | Dureza a | |
| LSL (Límite inferior de especificación) | 19 | 39 | 13 | 20.2 | 24.5 |
| USL (Límite superior de especificación) | 23 | 41 | 17 | 23.8 | 27.5 |
| Objetivo | 21 | 40 | 15 | 22 | 26 |
Las unidades utilizadas para cada especificación son las siguientes:

Es importante conocer el comportamiento de cada variable del proceso. Por lo tanto, se analizó la distribución de los datos para las dos fases, obteniendo:
Para la Fase I:
- Se estableció como hipótesis inicial H0=Los datos se distribuyen normalmente. Posteriormente se examinó la normalidad mediante el histograma de cada una de las variables (ver Figura 1). Por el tamaño y ubicación de las clases, se aprecia que la mayoría de los datos se concentran en el centro. Así mismo, al ajustar la curva de una distribución normal sobre cada histograma se puede observar que no existe una asimetría significativa. A esto se agrega que no se presentan colas largas, es decir, no se detectan valores atípicos considerables. Por lo tanto, se concluye que no existe evidencia visual para rechazar la hipótesis inicial. Los valores exactos para la media, dispersión estándar y varianza se muestran en la tabla 2.
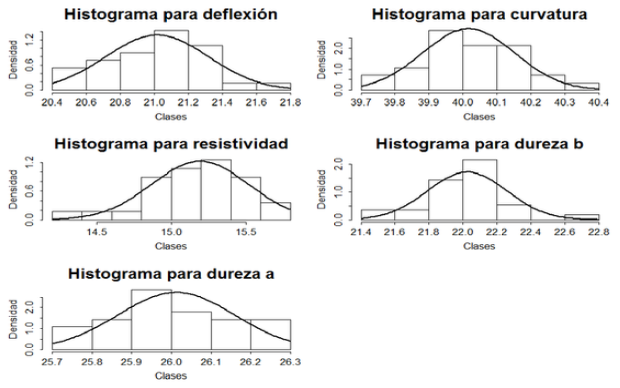
Figura 1. Histograma de las variables individuales. Fuente: Elaboración propia.
Tabla 2. Medidas de tendencia central y dispersión para cada una de las variables analizadas
| Deflexión | Curvatura | Resistividad | Dureza b | Dureza a | |
| Media | 21.01607 | 40.01607 | 15.19214 | 22.02393 | 26.01214 |
| Desviación estándar | 0.3031115 | 0.1361736 | 0.3260125 | 0.2333228 | 0.1465494 |
| Varianza | 0.09187659 | 0.01854325 | 0.1062841 | 0.05443955 | 0.02147672 |
- La matriz de dispersión de cada variable se ilustra en la Figura 2. En diagonal se muestra la distribución de cada variable, mientras que fuera de la diagonal se ubican gráficos de dispersión para cada par de variables. Los pares de variables con mayor dispersión son: deflexión y resistividad; curvatura y resistividad; dureza b y deflexión; dureza a y deflexión. Por otro lado, la aplicación de la prueba de Mardia generó un valor de sesgo de 6.982112 con un p-valor igual a 0.585327, mientras que la curtosis es 33.77 con un p-valor de 0.3490892. Luego, dados los p-valores de la asimetría y la curtosis, no hay evidencia para rechazar la normalidad.
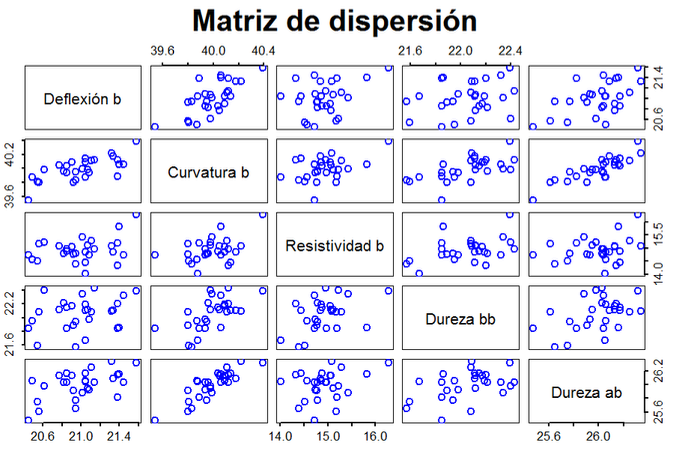
Figura 2. Matriz de dispersión entre las variables. Fuente: Elaboración propia.
- Para determinar el estado y la capacidad del proceso, primero se realizó un análisis de componentes principales, del cual se obtuvo que los Componentes 1 y 2 representan el 80.61% de variabilidad (Figura 3). Las dos variables de mayor importancia son la deflexión y la curvatura, que corresponden a las componentes 1 y 2 respectivamente. Representan un 58.09 % y un 22.51 % de la variabilidad total del proceso. Las variables de menor importancia son las restantes mencionadas en la Tabla 1 (Resistividad, Dureza a y Dureza b):
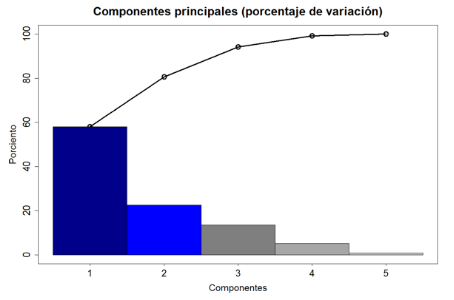
Figura 3. Diagrama de Pareto que muestra el porcentaje de variación de las componentes principales. Fuente: Elaboración propia.
- Una vez determinados los componentes principales para cada fase, se aplicó control estadístico multivariado de procesos mediante la implementación de la elipse de control y el gráfico de control T2 de Hotelling. En la elipse de control (Figura 4) se observó que no existen puntos fuera de esta, lo que significa que, de acuerdo con Santos-Fernández, no hay evidencia de causas especiales y, por lo tanto, se puede decir que el proceso se encuentra en control⁷.
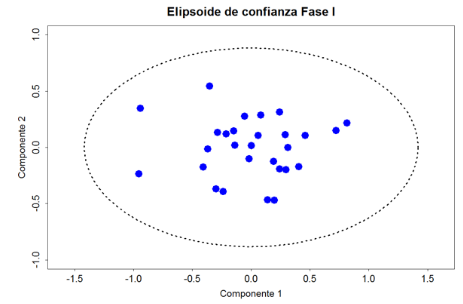
Figura 4. Elipse de confianza para los puntos de los dos componentes principales. Fuente: Elaboración propia.
- El Gráfico de control T2 de Hotelling( Figura 5) también muestra que todos los puntos se encuentran bajo el límite de control superior.
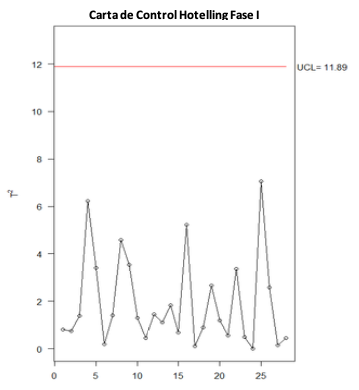
Figura 5. Gráfico de control T2de Hotelling para los componentes principales.
- Por último, se calcularon los índices de capacidad multivariados basados en PCA. Estos, indicaron que la capacidad potencial del proceso fue adecuada, al obtener un índice MCp mayor a 1.33. Mientras que la capacidad real del proceso resultó parcialmente adecuada, ya que los índices MCpk y MCpm tuvieron valores entre 1 y 1.33.
Para la Fase II:
En la Figura 6 se muestran los histogramas correspondientes a cada una de las variables analizadas en la Fase II. En este caso también se observa mayor concentración de los datos en el centro. Con el ajuste de la curva de una distribución normal (Figura 6) sobre cada histograma se puede notar que no existe una asimetría significativa, ni colas largas. Por lo tanto, se podría decir que las variables se distribuyen normalmente. Los valores exactos para la media, desviación estándar y varianza se muestran en la Tabla 3.
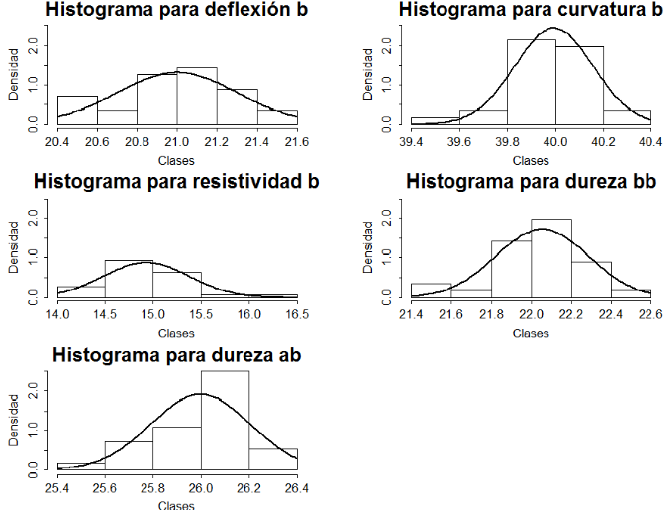
Figura 6. Histograma de las variables individuales para la Fase II. Fuente. Elaboración propia
Tabla 3. Medidas de tendencia central y dispersión para cada una de las variables analizadas en la Fase II
| Medidas de tendencia central y dispersión de cada variable | |||||
|
Deflexión b | Curvatura b | Resistividad b | Dureza bb | Dureza ab |
| Media | 21 | 39.99393 | 14.92714 | 22.05393 | 25.9975 |
| Desviación estándar | 0.3050076 | 0.1646622 | 0.4537323 | 0.2314742 | 0.2084799 |
| Varianza | 0.09302963 | 0.02711362 | 0.205873 | 0.05358029 | 0.04346389 |
- Para analizar la normalidad multivariable, se aplicó nuevamente la prueba de Mardia. En este caso la prueba arroja un valor de sesgo de 6.950879 con un p-valor igual a 0.5924351, mientras que la curtosis es 31.74321 con un p-valor de 0.1515315. Luego, dados los p-valores de la asimetría y la curtosis, no hay evidencia para rechazar la normalidad.
En la Figura 7 se muestra la matriz de dispersión. Para esta fase, se obtuvo que los pares de variables con mayor dispersión son: deflexión b y resistividad b; curvatura b y resistividad b; resistividad b y deflexión b; dureza bb y deflexión b; dureza ab y deflexión b.
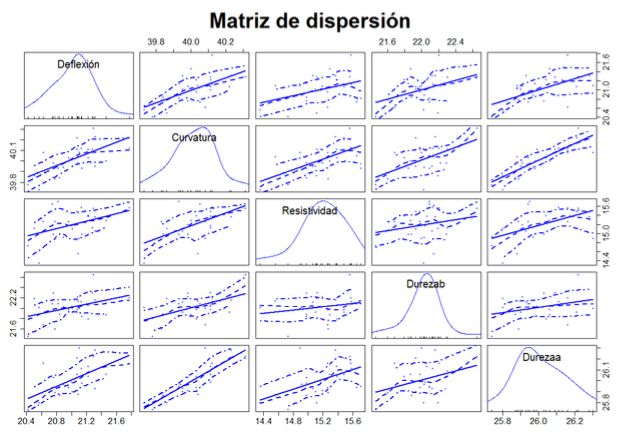
Figura 7. Matriz de dispersión entre las variables para la Fase II. Fuente: Elaboración propia.
- Del análisis de componentes principales en la Fase I, se obtuvo que los Componentes 1 y 2 representan el 83.85% de variabilidad (Figura 8).
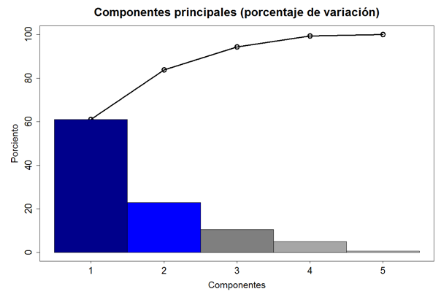
Figura 8. Diagrama de Pareto que muestra el porcentaje de variación de las componentes principales en la Fase II. Fuente: Elaboración propia
- Con base en el elipsoide de confianza construido en la Fase I, se agregan los datos correspondientes a los componentes principales de la Fase II (representados por las “x“ en la Figura 9). Se observa entonces, que el dato 18 se encuentra fuera de la elipse de confianza, lo que muestra evidencia de causas especiales y por lo tanto de un proceso que no está en control estadístico.
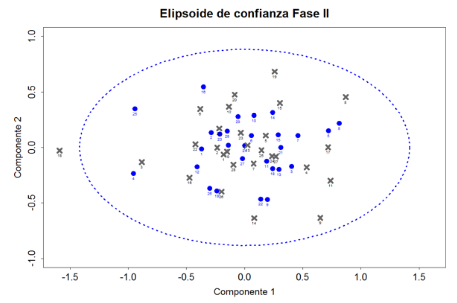
Figura 9. Elipse de confianza para las componentes principales de la Fase II. Fuente: Elaboración propia
- En la Figura 10 se muestran los gráficos de control T2 de Hotelling en la Fase I y la Fase II. Se puede notar nuevamente que el dato 18 se encuentra sobre el límite de control superior, con lo cual se confirma que hay evidencia de causas especiales. Por lo tanto, se puede decir que el proceso en la Fase II no se encuentra en control estadístico.
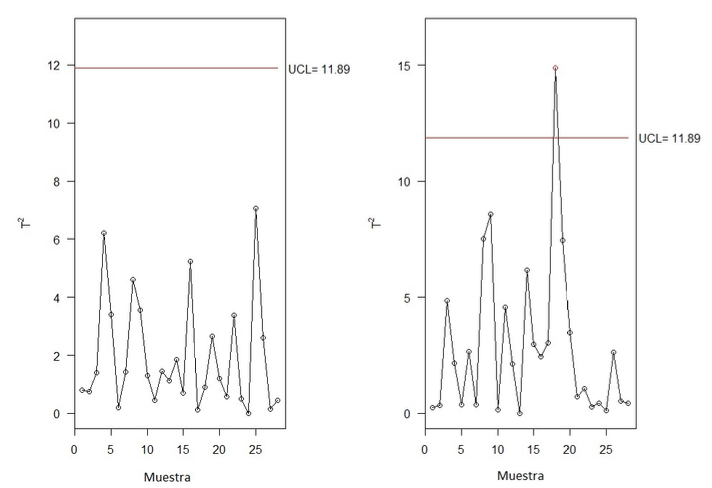
Figura 10. Gráfico de control T2de Hotelling para las componentes principales de la Fase II. Fuente: Elaboración propia
- Los índices de capacidad multivariados basados en PCA para esta fase, mostraron que la capacidad potencial y real son adecuadas, ya que los índices de capacidad MCp , MCpk y MCpm fueron mayores que 1.33.
Discusión
La aplicación del análisis de componentes en las dos fases contribuyó de manera positiva a la generación de los gráficos de control y al cálculo de los índices de capacidad del proceso. El problema de trabajar con 5 variables se redujo considerablemente al trabajar solo con dos componentes que representaron más del 80 % de la variabilidad del proceso, pasando así a un caso de análisis bivariado.
Los resultados obtenidos de la implementación del MSPC basado en PCA, permiten al grupo de control de calidad investigar cuáles son las causas especiales que puedan estar contribuyendo a que el proceso no se encuentre bajo control, para poder eliminarlas. Además, considerando los valores calculados de los índices de capacidad (proceso con capacidad aceptable) en la Fase II, se debe poner atención en las acciones de mejora que se implementaron durante el periodo de tiempo entre la Fase I y la Fase II, para controlar que continúe. Así mismo, integrar nuevas acciones que puedan contribuir a un incremento aún mayor de la capacidad del proceso.
Conclusiones
La implementación adecuada del control estadístico de procesos genera importantes mejoras en la detección de causas especiales de variabilidad, y como consecuencia va directamente relacionado con el incremento de la calidad de los productos y procesos. Además, las normas del Sistemas de Gestión de la Calidad establecen como requisito que las empresas realicen el control de sus procesos oportuna y adecuadamente. Por lo tanto, el control estadístico de procesos debería aplicarse de forma univariada cuando así sea suficiente. Sin embargo, ante la presencia de un número muy grande de variables se recomienda aplicar el control estadístico multivariado de procesos, situación en la cual, no es necesario trabajar con todo el conjunto de variables, sino solo una fracción, aplicando PCA.
El uso de métodos como el PCA, resulta de bastante utilidad para aplicar las técnicas multivariadas de control estadístico de procesos. Debido a que, si la correlación entre las variables es alta, se podría generar pérdida de información significativa para conocer el estado del proceso. Por otro lado, bajo las mismas condiciones, el conjunto de las componentes, que proporcionen la mayor información sobre la variación del proceso podría reducirse bastante y ser más fácil de analizar.
La realización de esta investigación deja camino para seguir aplicando otros métodos que pueden generar un análisis más completo, y que por limitación de recursos no se realizaron.
Entre las aplicaciones futuras se encuentra: Usar alguno de los métodos de descomposición para saber con mayor exactitud cuál o cuáles de las características de calidad están generando las causas especiales dentro del proceso de producción del bimetal. El método más aceptado es el de descomponer la estadística T2 en partes independientes propuesto por Mason y Young8.
Referencias
1. ANCHIRAICO, William R. Métodos multivariantes en control estadístico de la calidad [Trabajo monográfico de pregrado]. Lima, Perú: Universidad Nacional Mayor de San Marcos, 2003.
2. CAMACHO, J., PÉREZ- Villegas, A., GARCÍA- Teodoro, P., MACIÁ-Fernández, G. PCA- based multivariate statistical network monitoring for anomaly detection. Revista Computers & security [en línea]. Volumen 29, junio 2016. [fecha de consulta: 13 de mayo 2019]. Disponible en https://www.sciencedirect.com/science/article/pii/S0167404816300116
3. MOSQUERA Jaime; OLAYA, Javier y ESCOBAR, Rubria. Aplicación del control estadístico multivariante en un proceso de extrusión de película plástica. Revista Scientia et Technica [en línea]. Volumen 1, 2007, n 37. [Fecha de consulta: 13 de mayo 2019]. Disponible en http://revistas.utp.edu.co/index.php/revistaciencia/article/view/4115 . ISSN 0122-1701.
4. ISO (2015). ISO 9001-2015 Sistemas de gestión de la calidad — Requisitos. [Fecha de consulta: 24 de abril de 2019]. Disponible en https://www.bps.gub.uy/bps/file/13060/1/normativa-internacional-iso-9001.2015.pdf
5. MARCUERQUIAGA, Agustín. IATF 16949:2016. Especificación Técnica de calidad para industria automoción. [En línea]. 2017 [Fecha de consulta: 24 de abril de 2019]. Disponible en http://appi-a.com/wp-content/uploads/2017/06/20170531_INTERTEK_1NORMA.IATF16949.pdf
6. RENCHER, A. C. (2003). Methods of multivariate analysis. [En línea]. (2da. ed.). Estados Unidos de América: John Wiley & Sons, WILEY [Fecha de consulta: 18 de abril 2019]. Disponible en http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.905.8328&rep=rep1&type=pdf
7. SANTOS-FERNÁNDEZ, E. Multivariate statistical quality control using R. Springer Science & Business Media, vol. 14. Santa Clara, Cuba; 2012. 22-25 pp. ISBN 978-1-4614-5452-6.
8. MASON, R. L., y YOUNG, J. C. Multivariate statistical process control with industrial application, 2002. [Fecha de consulta: 17 de mayo 2019]. Disponible en https://books.google.com.mx/books?hl=es&lr=&id=0ST3luLyUMsC&oi=fnd&pg=PR2&dq=Multivariate+statistical+process+control+with+industrial+applications.&ots=3GOggZycvp&sig=qLWwOCGcIqSy-hbf8pjQcUDsE54#v=onepage&q=Multivariate%20statistical%20process%20control%20with%20industrial%20applications.&f=false



