En este artículo de investigación, se propone un controlador y un observador no lineal de tres grados de libertad para velocidad lateral controlada y torque de neumáticos por retroalimentación de estados, en comparación con un control PID (proporcional integral derivativo), aplicando una función de Lyapunov. Este trabajo muestra el desarrollo matemático de las estimaciones que se enviarán a los algoritmos de dos controles activos no lineales (retroalimentación de estado y PID), utilizando los resultados de las simulaciones en Matlab-Simulink del par de los neumáticos, de las velocidades lateral y angular de viraje, desde la medición de la velocidad longitudinal, con ganancias dinámicas a partir de la entrada de maniobra de dirección por parte del conductor bajo la norma internacional ISO 7401/2011, concluyendo que el observador es robusto y tiene eficiencia de ahorro en el par de los neumáticos, incluso con condiciones variables de fricción neumático- suelo.

Palabras clave: controlador, observador, Lyapunov, torque.

In this research paper, a three degree of freedom non linear controller and observer is proposed for controlled lateral speed and tire torque by state feedback, compared to PID (proportional integral derivative) control, applying a Lyapunov function. This work shows the mathematical development of the estimates that will be sent to the algorithms of two non linear active controls (state feedback and PID), using the results of the Matlab-Simulink simulations of the pair of tires, lateral speeds and turning angle, from the measurement of longitudinal speed, with dynamic gains from the steering maneuver input by the driver under the international standard ISO 7401/2011, concluding that the observer is robust and has saving efficiency in the pair of tires, even with varying tire-ground friction conditions.

Keywords: controller, observer, Lyapunov, torque.

El control activo en un vehículo puede establecer una ayuda al conductor o conductora en las maniobras que se realizan al automóvil, incrementando de manera más segura su maniobrabilidad, especialmente en situaciones críticas. Estas acciones activas incluyen la estabilidad de viraje^{1, 2}, sistemas de frenado^{3, 4}, la suspensión^{5, 6}, adherencia de las llantas al suelo^{7, 8} y el control integrado del automóvil^{9, 10}.

Se han investigado diversos enfoques de control en estos sistemas activos. En Zhang et al.¹¹ (2019) se toma en cuenta el coeficiente de adhesión llanta-suelo mediante un control robusto de antibloqueo en los frenos ABS con la asistencia de un sistema de suspensión activa (ASS). El análisis en las partes y componentes del sistema de frenado también han sido estudiados para prevenir la severidad y criticidad en las fallas de los componentes con la finalidad de reducir costos de mantenimiento¹².

Otras investigaciones se han centrado en los sistemas de recuperación de energía con algunos controles predictivos y neuro-difusos relacionando el frenado y la suspensión¹³. Además se establecen estudios importantes para mejorar el confort y la estabilidad en las vibraciones del vehículo, por lo que se han investigado diferentes enfoques de control basado en modelos, en señales de retroalimentación y control óptimo. Como en Li et al. (2017)¹⁴, utilizan un controlador para mejorar los movimientos pitch, y roll en sistemas no lineales con disturbios, utilizando control proporcional derivativo (PD) o fuzzy para las fuerzas de los actuadores (amortiguadores). Las suspensiones hidráulicas-electrónicas con sistema de aire pueden ser ajustadas por un controlador, por ejemplo el difuso, que supera a las suspensiones pasivas, reflejándose en la maniobrabilidad y confort de viaje en el automóvil¹⁵, sin olvidar que en la actualidad se proponen sistemas de control doble integrativo, lo cual activa en la suspensión dos actuadores hidráulicos con un controlador activo¹⁶. Por lo anterior, tanto la suspensión como el frenado deben considerarse al mismo tiempo para la estabilidad en condiciones de subviraje y sobreviraje. En Nahidi et al. (2017)¹⁷ desarrollan un sistema de control modular para los automóviles eléctricos (EV) y mejoran la estabilidad en los movimientos longitudinales y laterales del vehículo. En Lenzo et al. (2017 y 2021)^18,19 consideran ángulos slips (deslizamientos) en casos de sobreviraje para sistemas de una entrada simple una salida simple (SISO). Sin embargo, para los vehículos eléctricos de motores independientes en rueda, el movimiento longitudinal y lateral puede ser controlado por la distribución de manejo y torque de frenado regenerativo para sistemas multi-entrada multi-salida (MIMO) sobre todo en problemas del actuador (cuatro motores independientes de rueda) considerando ángulos slips en las llantas²⁰.

Debido a la complejidad en el control al utilizar varios motores y sistemas de propulsión distribuidos en las ruedas, se han implementado diversas estrategias de control para lograr la estabilidad deseada. En Xie et al. (2018)²¹ se utiliza control de lógica difusa y de retroalimentación de estados. De forma diferente, Tota y colaboradores/as (2018)²² implementan el control de par continuo presentado en las ruedas individuales mediante modos deslizantes. Por otro lado, Ataei et al. (2020)²³ presentan un controlador multiobjeto integrado para los vehículos eléctricos (EV) que puede considerarse un control slip en tracción y frenado, control de estabilidad lateral, maniobrabilidad y prevención roll (guiñada), unificándose para estas maniobras con un modelo de control predictivo (MPC).

Para la velocidad de rueda y la aceleración de chasís se puede estimar la máxima fricción neumático-suelo y se puede utilizar un control fuzzy (difuso) que usa la salida de torque para el control de ángulos slips, comprobando sus resultados en alguna plataforma Hardware-in-Loop (HiL)²⁴. Por lo tanto, en las diferentes propuestas de control para los motores de corriente continua Brushless se utilizan controladores de momento yaw (viraje), velocidad yaw y ángulos de deslizamiento slip para motores de las cuatro ruedas del EV, mediante controladores integrados como pueden ser PID, modos de deslizamiento, control adaptable y fuzzy con algoritmos de control con diferentes maniobras de conducción²⁵. Se ha considerado también el control integrado del vector de torque activo (ATV) y control de estabilidad electrónico (ESC)²⁶, además del momento de yaw directo (DYC), el cual utiliza el concepto de eficiencia de energía en el manejo del torque del motor²⁷, y el vector de torque trasero (TV), donde es habilitado para los motores eléctricos independientes en el eje trasero, controlando las dinámicas no lineales laterales del vehículo²⁸ o para la maniobrabilidad activa frontal (AFS)²⁹. Es importante comentar que, en algunas propuestas, las soluciones al estudio del torque del motor del EV o los motores de las ruedas del vehículo eléctrico son simuladas para la validación de los controles y observadores en plataformas comerciales como Matlab-Simulink^30,31,32, CarSim³³, u otras plataformas de diseño propio como Hardware-in-the-Loop (HiL)^{34, 35}, sin mencionar que en las diferentes investigaciones analizadas de esta introducción, no existe un estudio del torque en las llantas del EV donde se consideren las perturbaciones de viento y la aplicación de señales reales de sensores del automóvil para el diseño del control y estimación de estabilidad del vehículo eléctrico, por lo que en este artículo de investigación se propone un controlador de retroalimentación de estados considerando los disturbios de aire en un modelo matemático del EV con un coeficiente de fricción variable entre neumático-suelo y la estimación de la velocidad lateral, el torque y el momento yaw trasero del automóvil, comprobándose la estabilidad del observador con señales controladas mediante una función de Lyapunov, además de ofrecer una eficiencia de ahorro de torque del motor del eje trasero del vehículo eléctrico, comparándose con un controlador clásico PID de uso comercial.

Realizar un controlador con observador de retroalimentación de estados y compararlo con un control PID, utilizando un mismo sistema de referencia para la autonomía del automóvil, además de demostrar el ahorro de torque de las llantas del eje trasero del vehículo eléctrico.

Existen controladores y estimadores para las dinámicas y variables físicas del vehículo eléctrico en sistemas de autonomía vehicular de diferentes autores en áreas automotrices, pero sin la experiencia de transmitir el conocimiento de este tipo de controles a bajo costo y sin acceso universal al conocimiento.

A. Modelo matemático del vehículo

El modelo matemático del vehículo puede ser generalmente un cuerpo rígido moviéndose en un espacio de tres grados de libertad, conectado con la superficie terrestre a través de las llantas, el cual otorga un modelo de comportamiento no lineal. Los actuadores para esta aplicación son: conducción frontal activo (AFS, Active Front Steer) o conducción por cable (Sbw, Steer by Wire) y frenos activos. Esta complejidad de los sistemas no lineales puede ser disminuida considerando lo siguiente:

• Para estudiar la estabilidad y /o maniobrabilidad se analizarán solo las dinámicas de la velocidad lateral y velocidad angular de viraje. El actuador de frenos activos, M_z , servirá para crear una diferencia de fuerzas en el frenado, generando un momento de giro alrededor del eje z, afectando también las dinámicas de la velocidad lateral.
• La dinámica del ángulo pitch no es considerada. El sistema es un cuerpo rígido. Por lo tanto se puede tomar en cuenta la Figura 1, con las dinámicas no lineales del vehículo que se generan en el llamado modelo de la bicicleta³⁶.

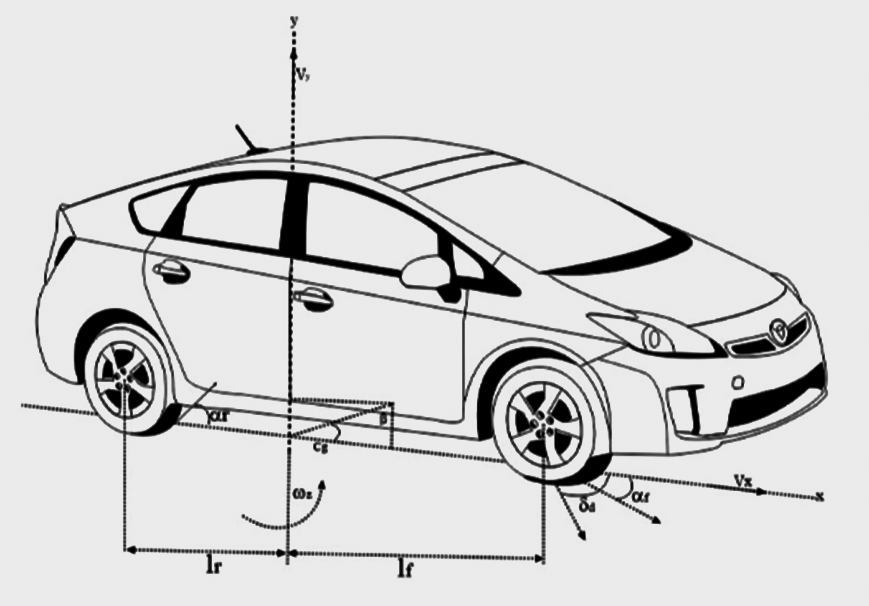
Figura 1. Modelo no lineal del vehículo (elaboración propia)

El modelo matemático propuesto se analiza a partir de las ecuaciones siguientes:

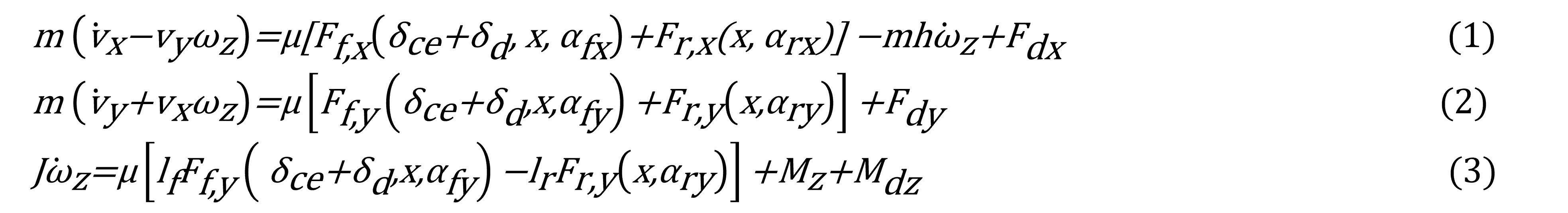
Donde, "m" es la masa del automóvil "(kg)" , "J" el momento de inercia del vehículo (kg∙m²) , "h" la altura del centro de gravedad (C.G) con respecto al suelo (m); l_f,l_r, longitud desde el centro del vehículo hacía la llanta frontal y trasera (m), r el radio rodante de la llanta (m) , v_x la velocidad longitudinal (m/s), v_y velocidad lateral (m/s), ω_z es la velocidad angular de viraje (rad) , x=[v_x,v_y,ω_z] el vector compacto del estado del vehículo, α_fy=α_fyl=α_fyr,α_ry=α_ryl=α_ryr los ángulos de deslizamiento laterales frontal y trasero de las llantas izquierda y derecha (rad) ; α_f,0, α_rx0 son los ángulos de deslizamiento lateral frontal y longitudinal trasero sin control respectivamente (rad) , α_fx=α_fxl=α_fxr,α_rx=α_rxl=α_rxr los ángulos de deslizamiento longitudinales frontal y trasero de las ruedas izquierda y derecha (rad), δ_ce,δ_d son componentes del ángulo de la llanta impuesto por el controlador y el conductor respectivamente (rad), M_z el momento de viraje resultado de los frenos activos (N∙m), μ es el coeficiente de fricción entre la llanta y el suelo, F_dx,F_dy son las fuerzas aerodinámicas longitudinal y lateral (N), M_dz es la perturbación aerodinámica externa de viraje (N∙m) , F_f,x , F_r,x son las fuerzas frontales y traseras longitudinales de las ruedas (N), F_f,y,F_r,y las fuerzas laterales frontal y trasera (N) en función del ángulo impuesto a las llantas frontales (δ=δ_d+δ_ce).

Además los ángulos de deslizamiento lateral de las llantas se definen de la siguiente manera:

También los ángulos de deslizamiento longitudinal se consideran de esta forma:

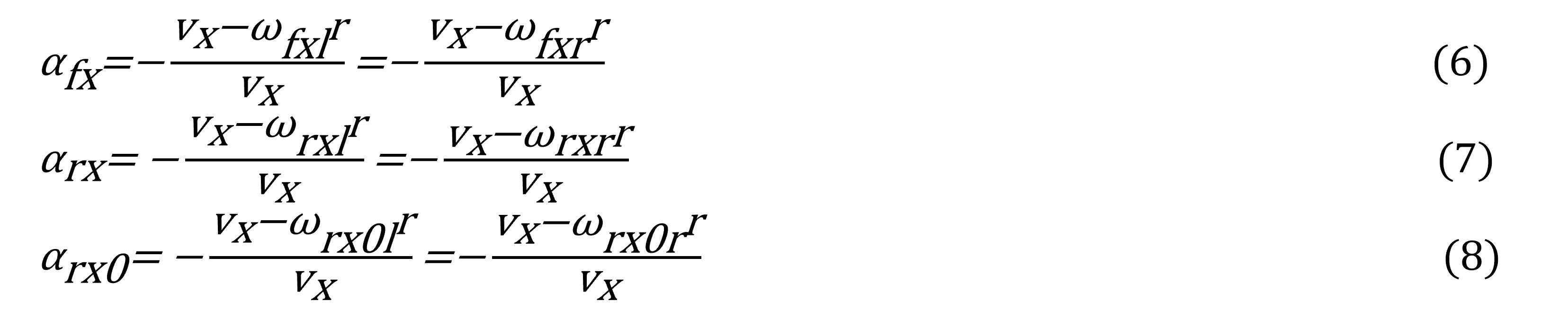
Además las aceleraciones angulares de las llantas traseras izquierda y derecha se establecen, proponiendo:

Considerando a ω_fxl ω_fxr , velocidades angulares frontales izquierda y derecha de las llantas controladas (rad), ω_rx0l ,ω_rx0r , velocidades de revoluciones en las ruedas traseras izquierda y derecha sin control (rad), T_n, el torque de manejo y frenado aplicado al neumático, T_n=M_z r/ T (N∙m), J_n , momento de inercia de la llanta (kg∙m²),T, ancho de la banda de rodadura del neumático (m), F_rxl , F_rxr , las fuerzas traseras longitudinales izquierda y derecha de la rueda respectivamente (F_rxl +F_rxr =F_r,x ) y F_rozl , F_rozr , las fuerzas de rozamiento para las llantas en el eje z (N) , con³⁷:

Y la fuerza normal F_roz=mg cos(α), analizando que α, sea el ángulo de pendiente del VE, que para nuestro caso está sobre una carretera plana, con α≈0 . Pero considerando la gravedad (g = 9.81m/s ² ). Y el coeficiente de arrastre que lo forma μ₀ , sugerido como asfalto promedio, además de μ₁=μ, como coeficiente para el efecto de la velocidad en cada llanta trasera.

B. Aerodinámica del vehículo

Los disturbios de viento que afectan la estabilidad del vehículo al moverse con respecto a las fuerzas longitudinales ( F_f,x = F_fxl + F_fxr ,F_r,x ), son la fuerza de perturbación de aire longitudinal F_dx , en dirección opuesta y con respecto a la fuerza lateral (F_f,y ,F_r,y ), también se aplica una fuerza inversa lateral de disturbio de aire F_dy. Dependiendo del análisis de perturbación de viento sobre el chasís del automóvil, un disturbio aerodinámico de viraje se crea, denominado M_dz. Para analizar los componentes del viento es necesario identificar un sistema de coordenadas (X,Y,Z), el cual es un punto sobre el vehículo paralelo a las coordenadas de la masa en suspensión del automóvil (x,y,z), con el desplazamiento lateral que se muestra en la Figura 2.

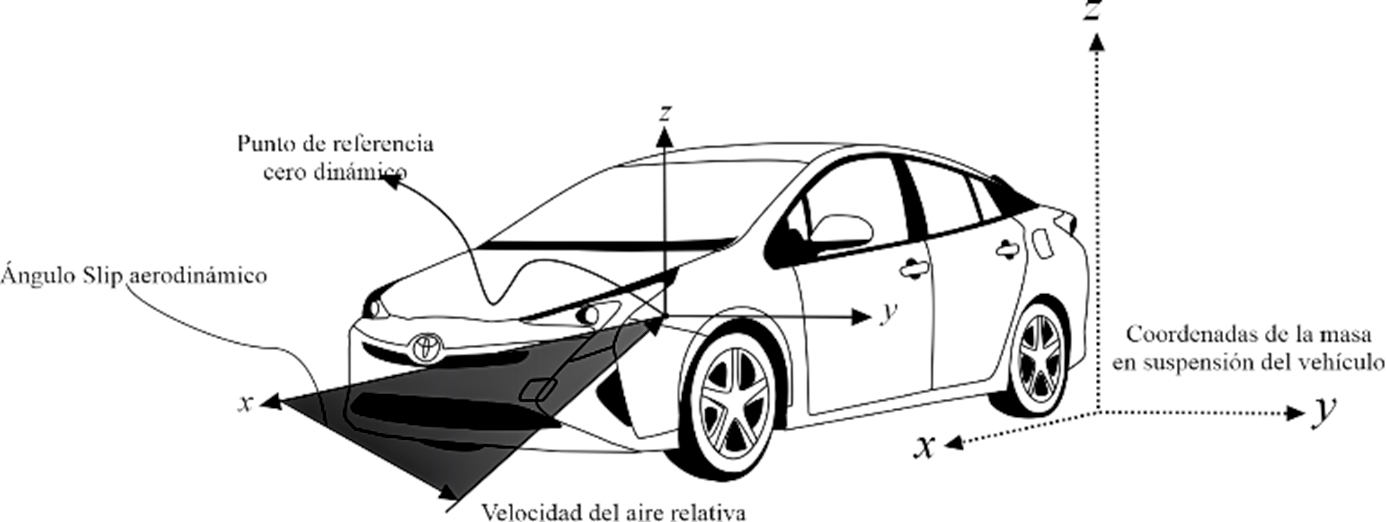
Figura 2. Punto de aerodinámica del vehículo (elaboración propia)

Las perturbaciones externas d pueden ser representadas como:

Considerando: A_s , superficie del vehículo (m² ); ρ es la densidad de masa de aire (kg/m³) , c_ψ coeficiente aerodinámico constante y v_w velocidad del aire (m/s). Por lo tanto los disturbios de aire se obtienen de la siguiente manera³⁸:

Donde A_s,f , A_s,l son la superficie frontal y lateral del vehículo (m² ), c_a,x , c_a,y son los coeficientes longitudinal, lateral aerodinámicos respectivamente y v_a,w,x , v_a,w,y , componentes de velocidad del viento en el eje x, y, sobre la masa en suspensión del vehículo. Además. en las plataforma Matlab-Simulink se utilizan estos parámetros de disturbio de aire para establecerlas en condiciones reales, como son la velocidad del viento (Vwind = v_w,0) con un ángulo global de viraje del aire (Yaw wind = ψ ), a partir de un ángulo de deslizamiento (slip) aerodinámico (Beta air = β₀) y velocidad relativa de viento (Vair), ver Tabla 1.

Tabla 1. Parámetros para las simulaciones de las perturbaciones de viento (elaboración propia)

vw,0 =28 m/s	β0 =-22.5°
As,f =2.59 m2	As,l =5.10 m2
ca,x =0.3	ca,y =0.6
ρ = 1.206 kg/ m3	va,w,z =0 m/s
ψ = 225°	"Vair = 185 km/h"

C. Diseño del controlador por retroalimentación de estados

Para la parte del controlador se consideran las ecuaciones (1), (2) y (3), del modelo matemático del VE en forma de espacio de estados como propuesta de control:

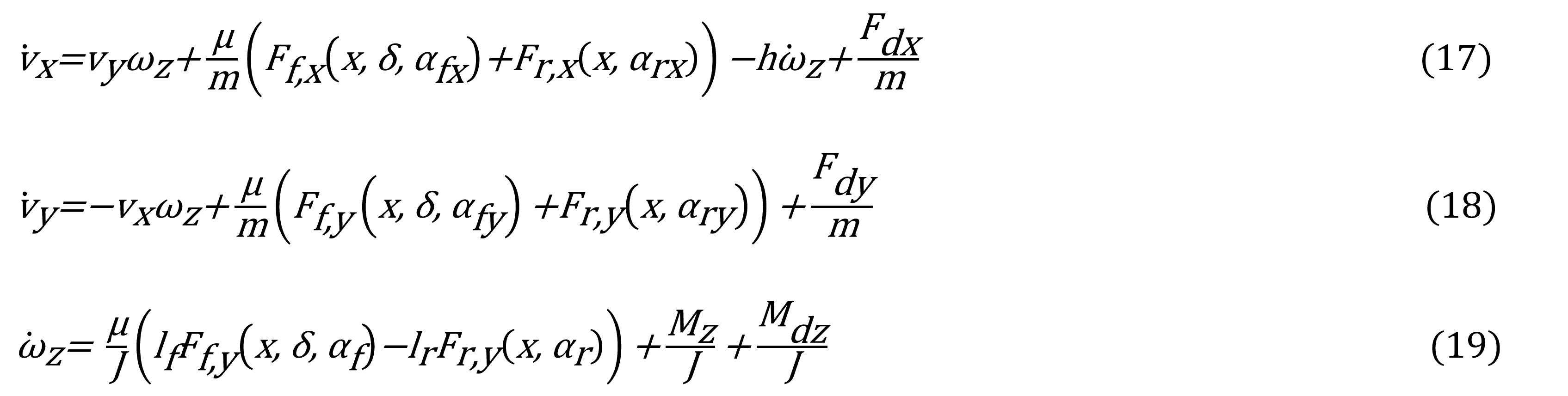
La aceleración lateral puede ser expresada usando la segunda ley de Newton en términos de las fuerzas laterales de las llantas.

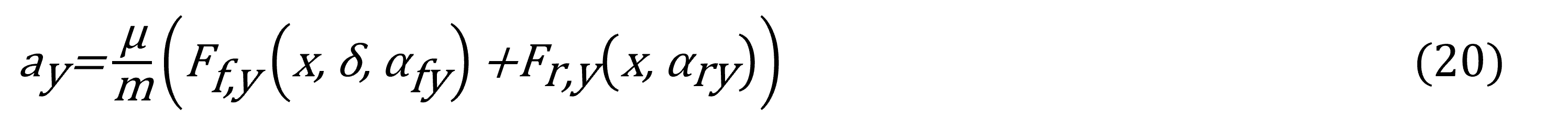
También la aceleración longitudinal se establece de la siguiente forma:

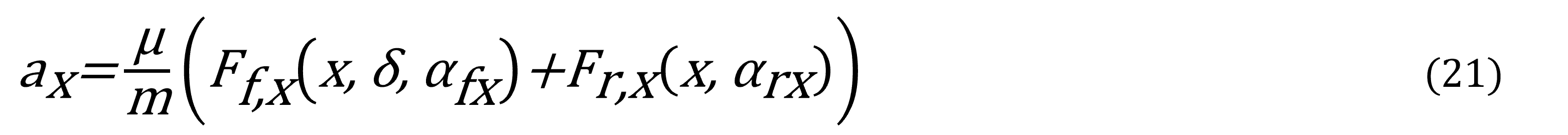
La fuerza lateral y longitudinal puede ser definida usando la fórmula mágica³⁹:

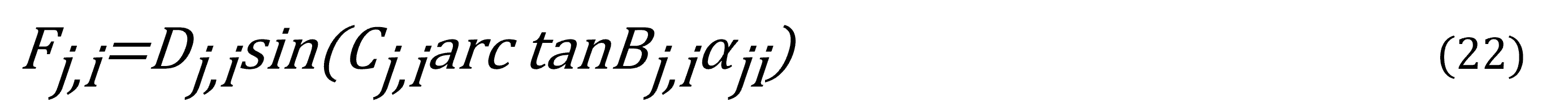
Con j=f,r, i=x,y. Las constantes B_j,i , C_j,i , D_j,i en (1), (2) y (3) son determinadas experimentalmente (ver Tabla 2). Las entradas de control serán consideradas como el resultado del momento de viraje de los frenos activos M_z, del torque aplicado a los neumáticos traseros T_n y la diferencia en las fuerzas laterales frontales y longitudinales traseras de las llantas del VE:

Además, la entrada de control para la dirección asistida en los neumáticos frontales será δ_ce , la cual puede ser determinada por (4) y (22), utilizando α_fy:

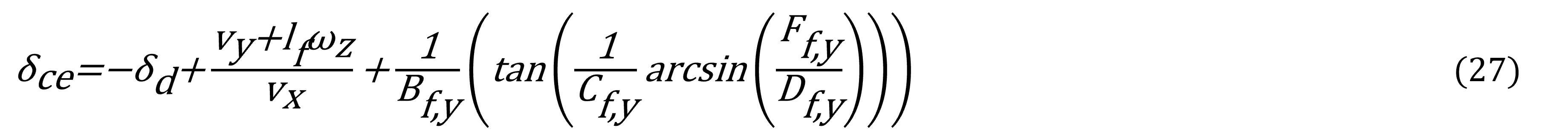
El principal objetivo del control es que la salida del sistema (v_x ,v_y , ω_z ), siga asintóticamente un sistema de referencia, el cual tiene como característica principal que sus derivadas son acotadas. El sistema de referencia es:

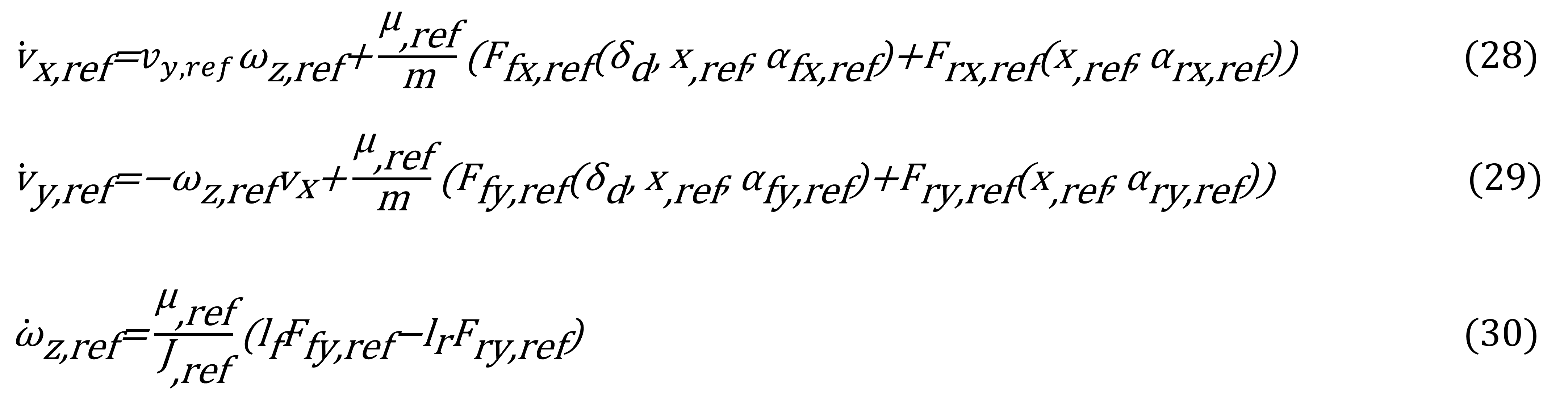
x_,ref (v_x,ref , v_y,ref ,ω_z,ref ) = Vector compacto de referencia del estado del vehículo. J_,ref =J, μ_,ref =μ, son parámetros apropiados y F_fy,ref , F_ry,ref , F_fx,ref, F_rx,ref (calculadas por ecuación 22), son curvas ideales dependiendo de:

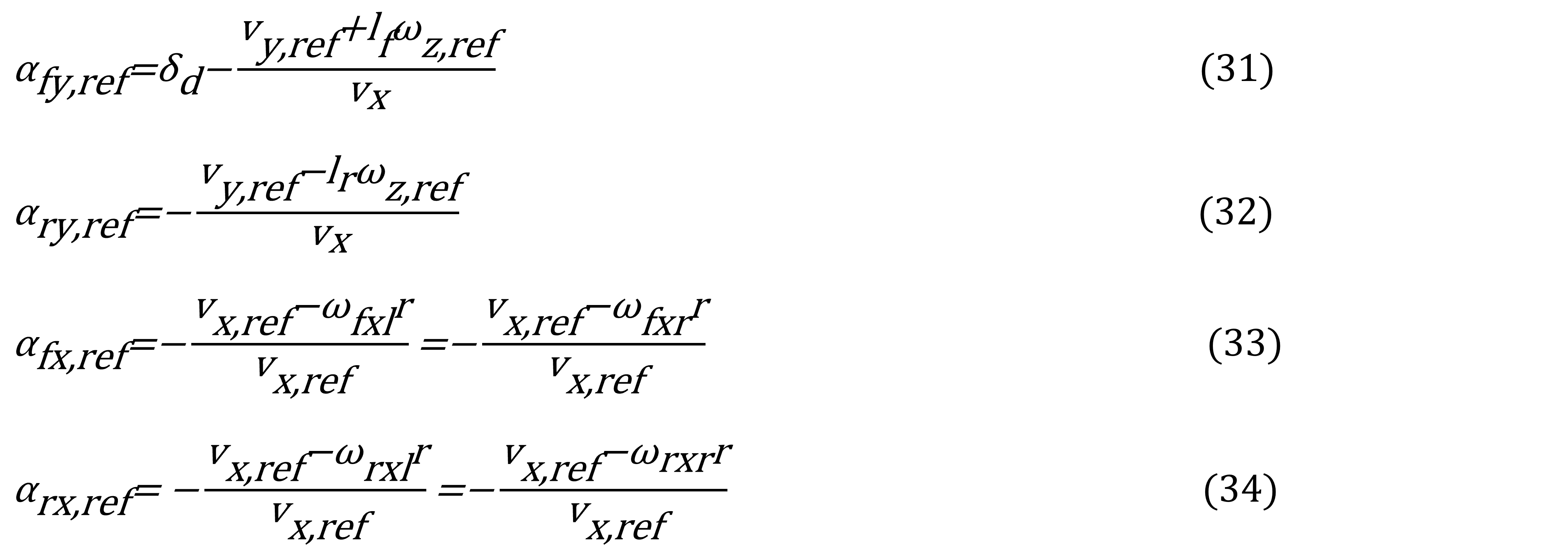
Para el diseño de control por linealización de retroalimentación de estados, el cual impondrá el comportamiento para las dinámicas de las velocidades lateral y de viraje, se realizará imponiendo la señal de referencia de (28), (29) y (30), a través de la implementación de las entradas ∆F_r,x , ∆F_f,y y M_z , por medio de la siguiente ley de control:

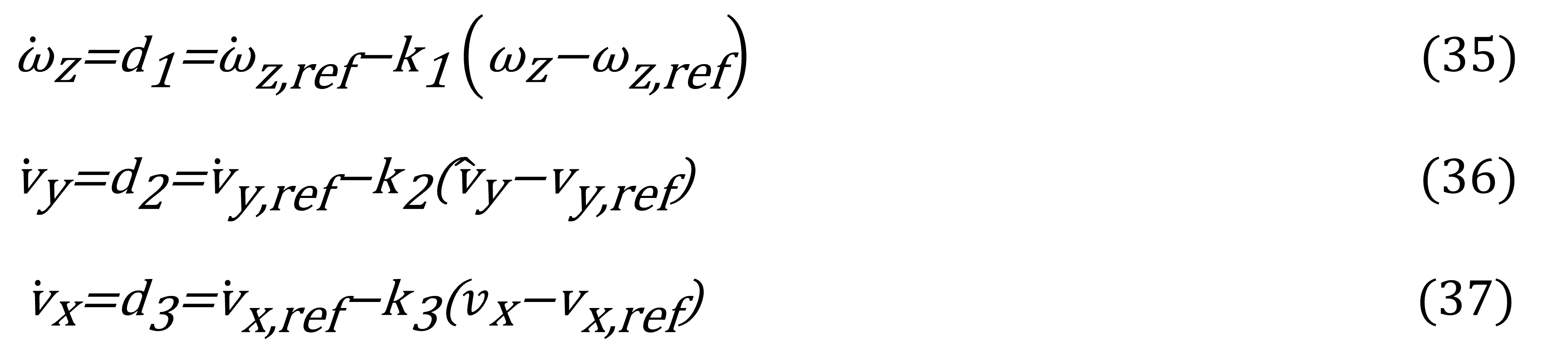
Donde k_ii>0,ii=1,2,3. Por lo tanto las entradas de control serán:

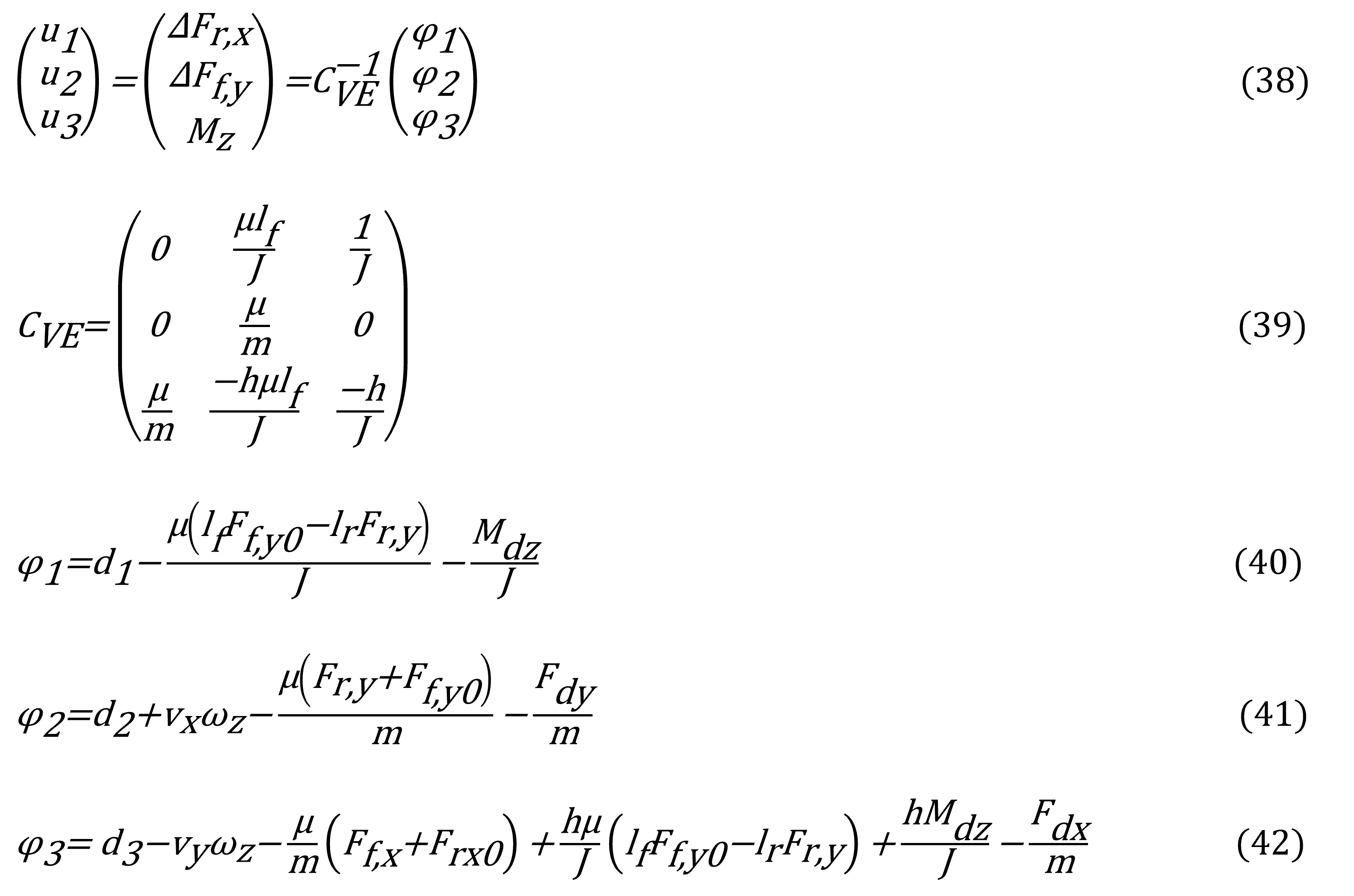
Una de las consideraciones que se deben de tomar en cuenta es la inversión de la matriz C_VE, donde la primera columna depende del parámetro μ, la cual será invertible si μ≠0 y su inverso:

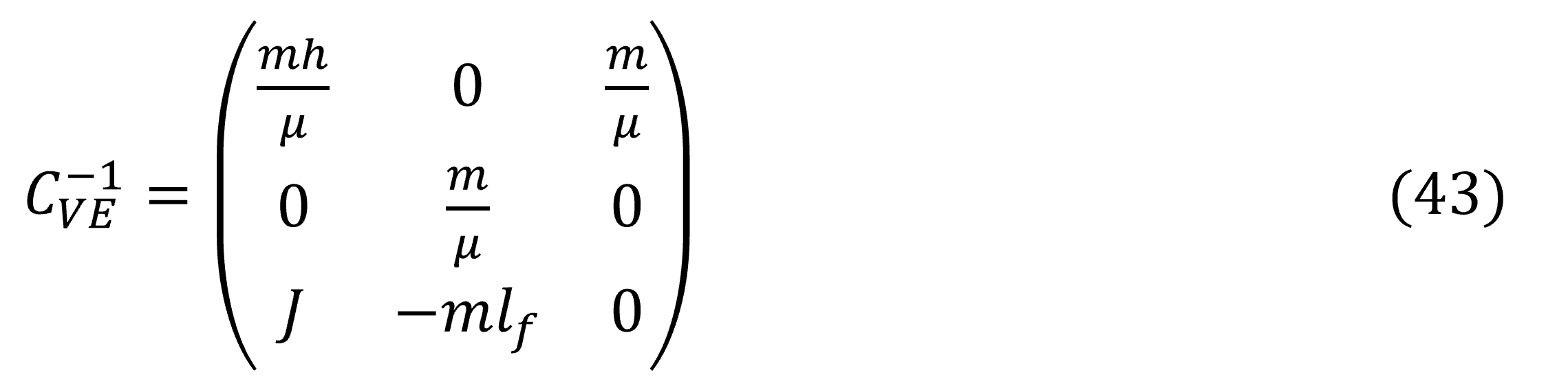
D. Diseño del observador por retroalimentación de estados

En algunas ocasiones no se tiene la medición de la velocidad lateral, por lo tanto es necesario diseñar un observador para estimar esta variable^40,41,42,43. La aplicación en el control activo de esta variable estimada v_y será establecida como:

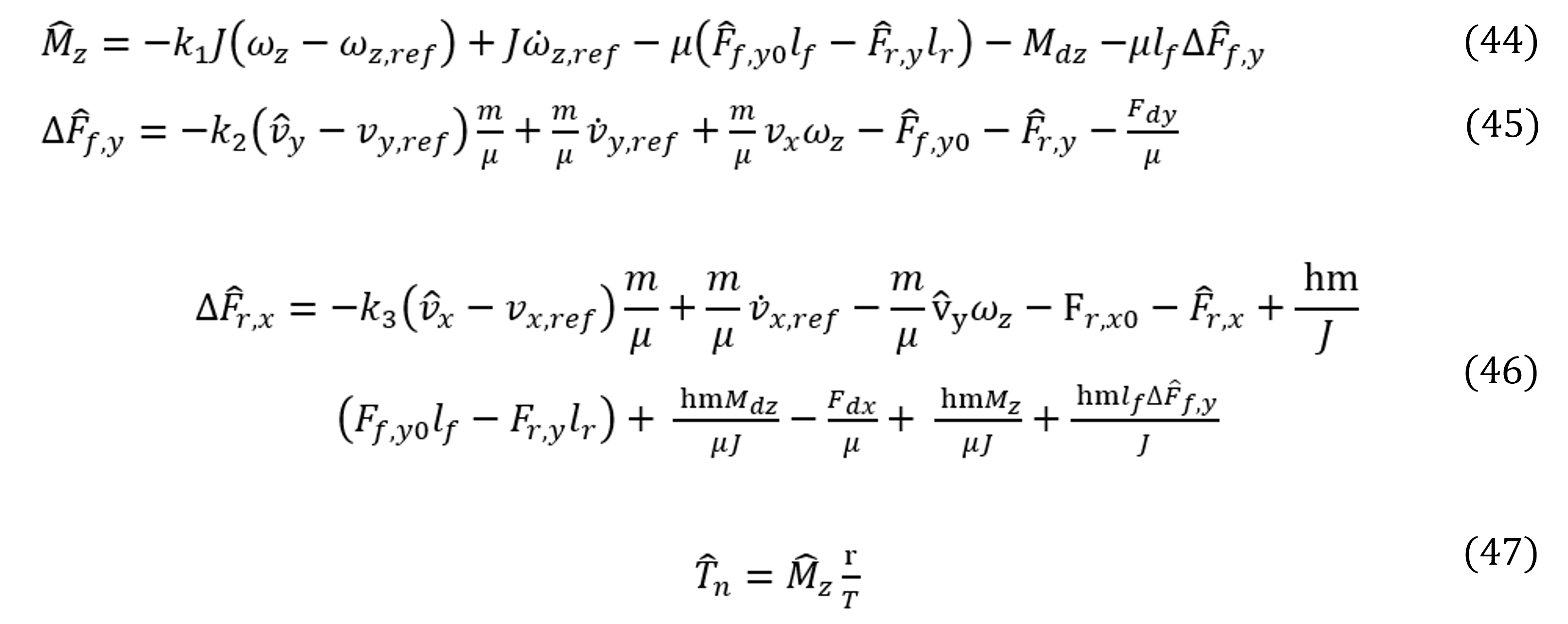
Considerando:

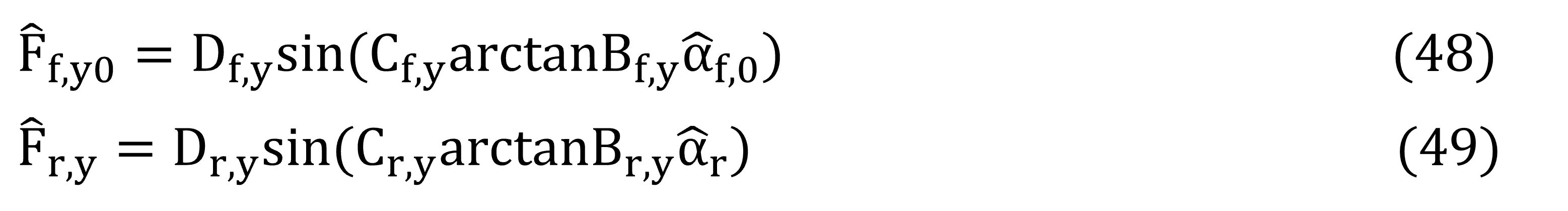
Estableciendo:

Continuando con la suposición que a_x, a_y, v_x, ω_fxl , ω_fxr , son medidas, siendo una hipótesis aceptable en vehículos modernos, usualmente equipados con los sensores necesarios, además de poder hacerse mediciones con instrumentos como el Scanner Otofix de Autel y el Osciloscopio-multímetro Hantek para observar las variables y dinámicas. La propuesta del observador no lineal para la velocidad lateral es realizada como una copia de la planta en ecuación (1) y (2):

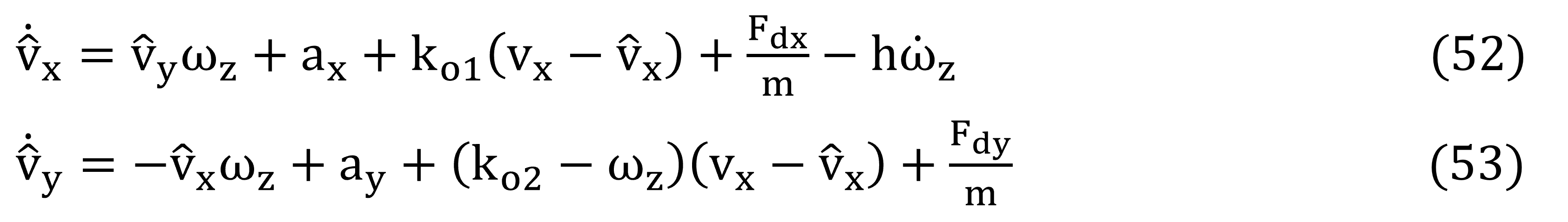
Donde k_o1,k_o2, son las ganancias del observador determinadas por las ecuaciones (1), (2) y (52), (53), necesitándose obtener los errores estimados:

Y los errores dinámicos:

Para (56) y (57) es lineal y variante en el tiempo el parámetro ω_z. Esto puede asegurar la convergencia exponencial de la estimación de errores, asumiendo que la velocidad angular yaw ω_z≠0, considerando que |ω_z |≤ω_{z , min} , un cierto valor mínimo (ω_z,min), para todo tiempo t≥0. Estas consideraciones físicas son razonables, porque el vehículo es un sistema de energía finito, donde la velocidad angular yaw mínima es acotada. En las maniobras de entrada del volante del conductor al automóvil, ω_z puede pasar a través de cero, pero no puede ser cero en un intervalo finito de tiempo y tampoco las fuerzas laterales de las llantas del vehículo, considerando que el automóvil no está estacionario.

El diseño de las ganancias k_o1, k_o2 son obtenidas utilizando la siguiente función candidata de Lyapunov:

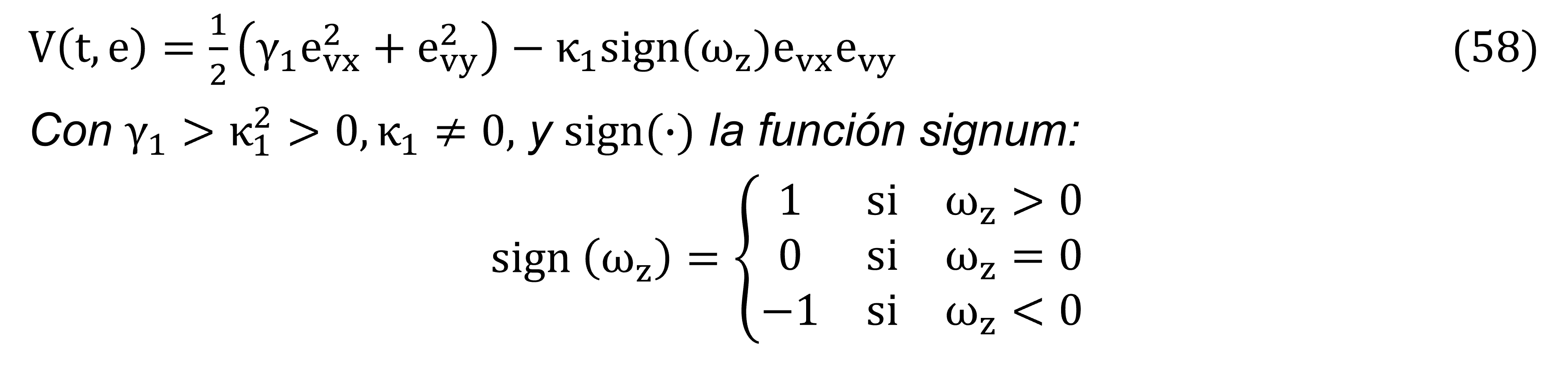
A partir de las consideraciones anteriores, se determina la derivada de la función candidata de Lyapunov en (58) y utilizando los errores dinámicos de (56) y (57), se obtiene lo siguiente:

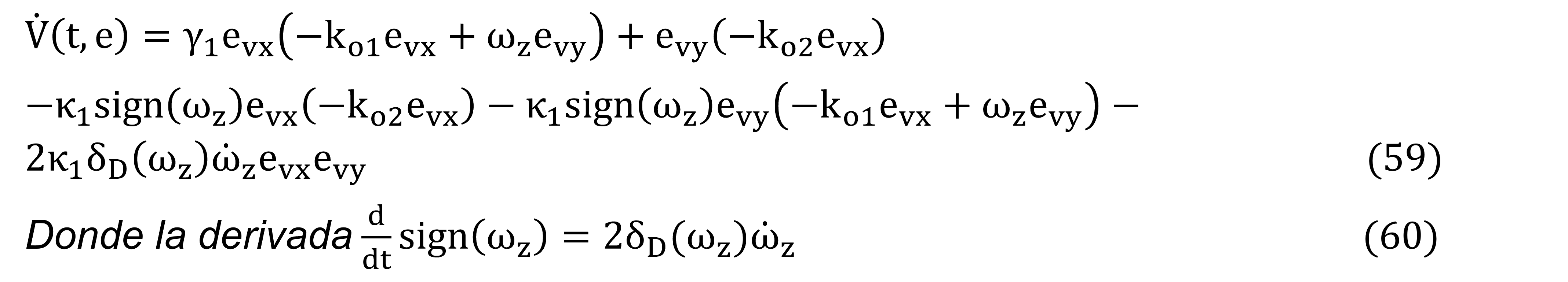
Y la distribución de Dirac en δ_D (ω_z), para |ω_z> |>0, se considera cero (δ_D (ω_Z )=0), obteniendo:

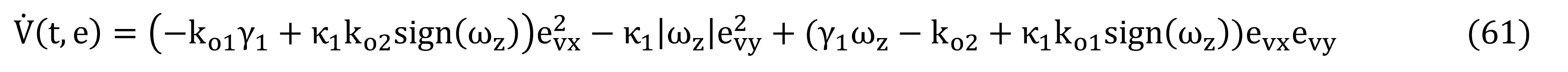
Esta ecuación (61) es resuelta por el método de Cramer para determinar las ganancias del observador:

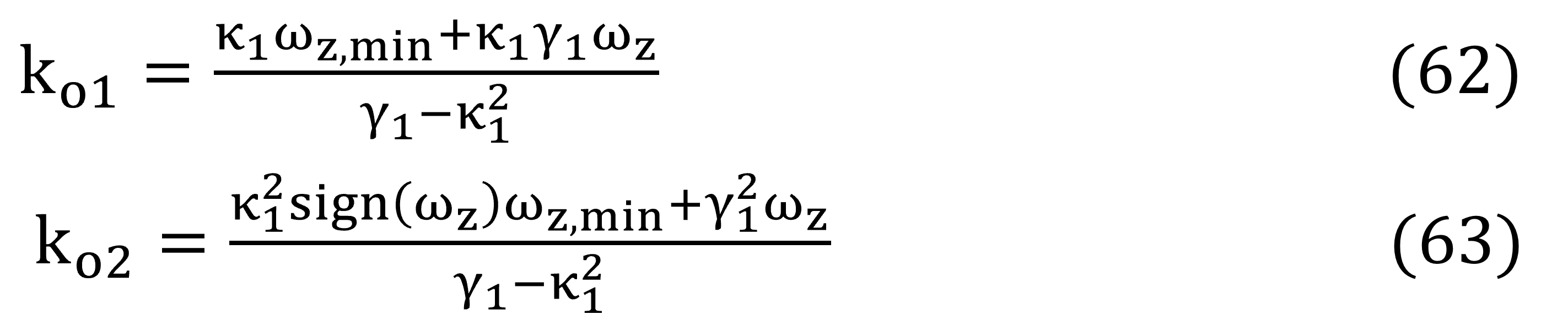
Estableciendo las ganancias (62) y (63), en la derivada de la función candidata (61), se tiene como resultado:

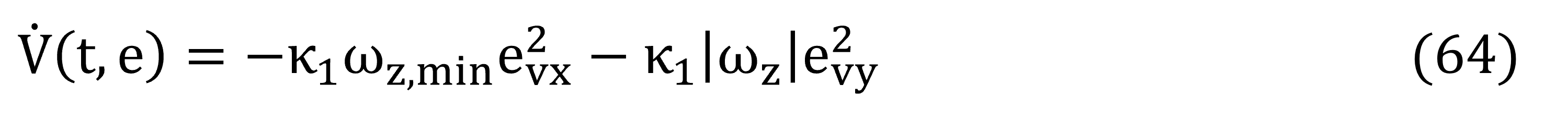
Los siguientes valores para (64) son propuestos:

Acotando en (64) con las condiciones de (65) y (66), la derivada de la función de Lyapunov será estable:

Enseguida se establecerá, para el control activo por retroalimentación de estados, diseñado en (35), (36) y (37), una comparación con un control PID, bajo condiciones similares.

E. Diseño del controlador activo PID

Para este controlador PID, la ley de control es establecida en (68), (69) y (70), utilizando los errores de la velocidad lateral (52) y velocidad angular de viraje (53):

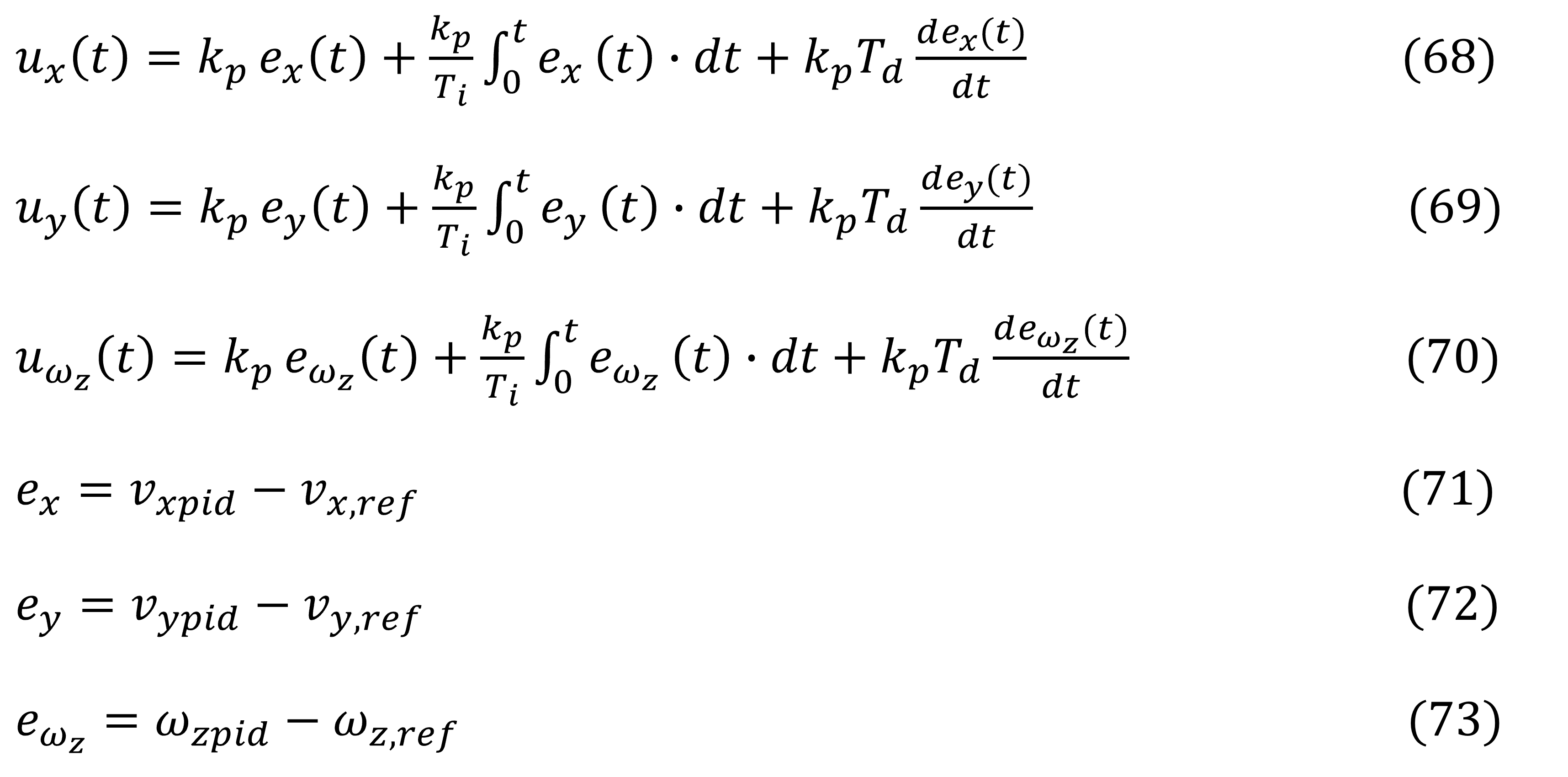
La planta a controlar es el modelo matemático en (17), (18) y (19), actualizando solamente sus subíndices para PID, como se puede ver en ecuaciones (74-76), con las entradas de control (77-79). Además del sistema de referencia en (28), (29) y (30).

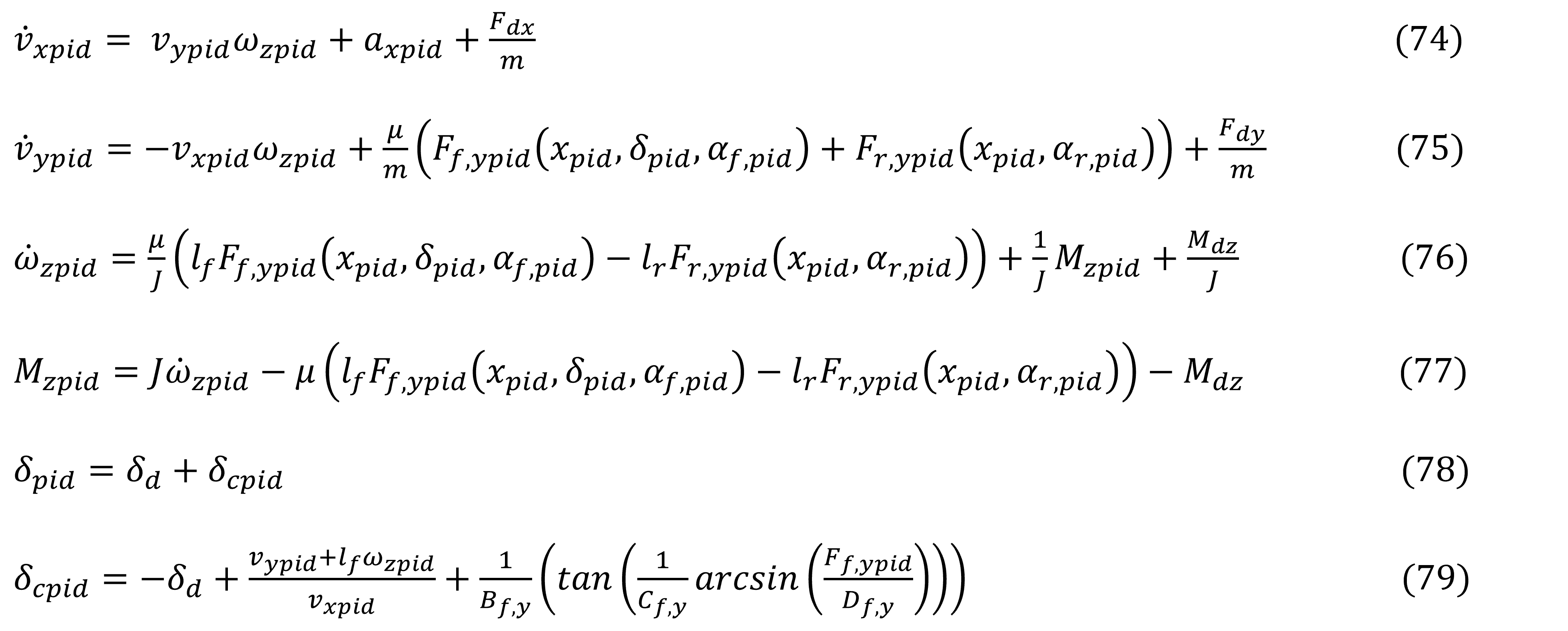
Tabla 2. Parámetros para las simulaciones en Matlab-Simulink (elaboración propia)

m = 1550 kg	Bf, x = 6.9	Bf, x, ref = 6.9
J = 3552 kg ∙ m2	Cf, x= 1.3	Cf,x,ref = 1.3
lr = 1.53 m	Df,x = 7500 N	Df,x,ref = 10000 N
lf = 1.38 m	Br,x = 7.1	Br, x, ref = 7.1
Br,y = 10	Cr,x = 1.6	Cr,x,ref = 1.6
Cr,y = 1.32	Dr,x = 7500 N	Dr,x,ref = 10000 N
Dr,y = 7834 N	kp = 100.475	Br,y,ref = 10
Bf,y = 6.9	Td = 0.00073	Cr,y,ref = 1.32
Cf,y = 1.78	Ti = 45.84383	Dr,y,ref = 10000 N
Df,y = 7240 N	Jn = 62 kg ∙ m2	Bf,y,ref = 6.9
T = 0.16 m	r = 0.2 m	Cf,y,ref = 1.78
μ0 = 0.9	h = 0.5 m	Df,y,ref = 10000 N

Maniobra en una dirección

Los siguientes resultados son para una maniobra ISO 7401, en la Figura 3. Y el coeficiente de fricción neumático-suelo de μ=0.9 (superficie seca, de 0s-10s), y (superficie mojada) a los 10 segundos (ver Figura 4). En la Figura 5, se muestran los valores de la velocidad lateral, donde la velocidad de control (la cual es por retroalimentación de estados) sigue a la velocidad lateral de referencia y al observador de mejor forma que la velocidad lateral con el control PID y la velocidad angular de viraje por retroalimentación de estados que sigue casi a la perfección a la velocidad angular de viraje de referencia, tiene menores oscilaciones que la velocidad de control PID, en Figura 6. Con los controladores en (18-19), (75-76), comparados con el sistema de referencia en (29-30). En las Figuras 5-7, se tienen los parámetros para, k₁=100, k₂=100, k₃=100, en (35-37), y para k_o1,k_o2, en (52-53), se está considerando γ₁=0.023, κ₁=0.15, λ_s=1, para el observador con dinámicas de control por retroalimentación de estados.

Nota: las figuras de la 3 a la 9 son de elaboración propia.

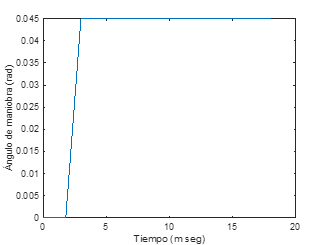
Figura 3. Señal δ_d del conductor (rad vs s)

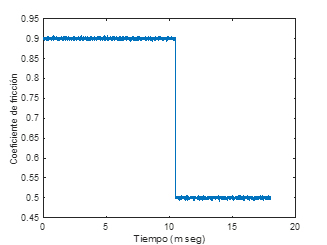
Figura 4. Coeficiente de fricción μ

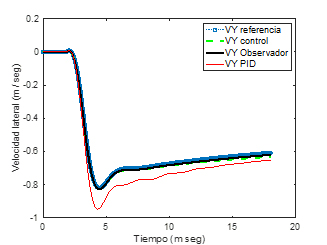
Figura 5. Velocidad lateral v_y,v_ypid ,v_y,ref, V̂_y (m/s vs s)

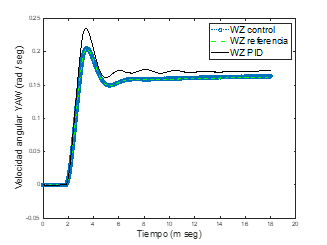
Figura 6. Velocidad angular de viraje ω_z ,ω _zpid ,ω_z,ref (rad vs s)

También los resultados para la velocidad longitudinal se inician con v_x=28m/s en la Figura 7, además se muestran los valores con el controlador PID que se desvía del valor de referencia, y del control por retroalimentación de estados, donde este último es estimado de manera correcta por el observador de retroalimentación de estados propuesto en este artículo de investigación, lo cual tiene como resultado un torque T_n estimado para las llantas traseras del vehículo eléctrico con una eficiencia de ahorro de torque considerable aún con las diferentes condiciones de coeficiente de fricción neumático-suelo (ver Figura 8) y el PID con T_npid en la Figura 9.

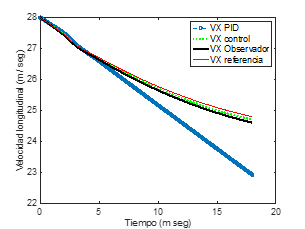
Figura 7. Velocidad longitudinal v_x , v_xpid , v_x,ref, V̂_x (m/s vs s)

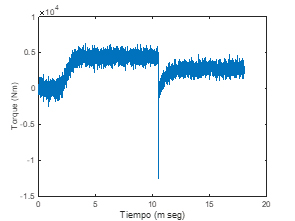
Fig. 8. Señal T_n de las llantas traseras (N∙m vs s)

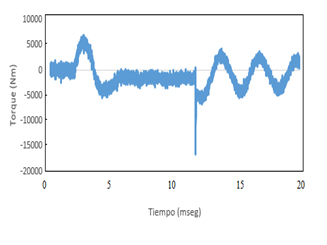
Figura 9. Señal T_npid de las llantas traseras (N∙m vs s)

Este trabajo de investigación se realiza con la finalidad de proponer un observador para la velocidad lateral, partiendo del modelo de la bicicleta, el cual se utiliza para el controlador de retro de estados y compararlo con el PID, como una idea original, al implementar un solo sistema de referencia para los dos controles activos de retroalimentación de estados y PID, obteniendo con ello algoritmos de entrada de control al automóvil, que producirán la señal del controlador(δ_ce,δ_cpid) para la dirección asistida automotriz del vehículo.

Se puede concluir que con la norma ISO 7401, el controlador PID tiene algunos problemas al controlar las variables y dinámicas del automóvil.

Finalmente se establece que los modos de control a recomendar para obtener un controlador-observador para aplicación a la dirección asistida automotriz, estudiados en este artículo de investigación, puede ser el de retroalimentación de estados, como una propuesta para ciertas situaciones de maniobra en el vehículo. Además de mencionar que estos controladores y observador de este artículo de investigación se pueden realizar con electrónica de bajo costo, siguiendo la técnica propuesta por Sandoval (2020)⁴³, para trabajarlos en forma experimental y compararlos con las plataformas comerciales de Matlab-Simulink, HIL de National Instruments o CarSim.

Se agradece a los talleres de la Zona Sur de Jalisco por los conceptos obtenidos en la utilización del Software Otofix de Autel y del equipo de medición Hantek.

1. ZHANG, Houzhong; Liang, J., Jiang, H., Cai, Y. y Xu, X. Stability Research of Distributed Drive Electric Vehicle by Adaptive Direct Yaw Moment Control. IEEE Access. [En línea]. Vol. 7 (1), pp. 106225-106237. 05 de agosto de 2019. [Fecha de consulta: 10 de marzo de 2024]. DOI: 10.1109/ACCESS.2019.2933016 ISSN: 2169-3536.
2. DE BERNARDIS, Martino; Rini, G., Bottiglione, F., Hartavi, A. E. y Sorniotti, A. On nonlinear model predictive direct yaw moment control for trailer sway mitigation. Vehicle Systems Dynamics. [En línea]. Vol. 61 (2), pp. 445-471. 09 de agosto de 2022. [Fecha de consulta: 10 de marzo de 2024]. DOI: 10.1080/00423114.2022.2054352 ISSN: 1744-5159.
3. CHUN-LIANG, Lin; Hao-Che, H. y Jia-Cheng, L. Active Control of Regenerative Brake for Electric Vehicles. Actuators. [En línea]. Vol. 7 (4), pp. 1-14. 01 de diciembre de 2018. [Fecha de consulta: 11 de marzo de 2024]. https://doi.org/10.3390/act7040084 ISSN: 2076-0825.
4. CHEN, Liqing; Li, Z., Yang, J. y Song, Y. Lateral Stability Control of Four-Wheel-Drive Electric Vehicle Based on Coordinated Control of Torque Distribution and ESP Differential Braking. Actuators. [En línea]. Vol. 10 (6), pp. 1-16. 18 de junio de 2021. [Fecha de consulta: 11 de marzo de 2024]. https://doi.org/10.3390/act10060135 ISSN: 2076-0825.
5. SOLIMAN, Ama y Kaldas, MMS. Semi-active suspension systems from research to mass-market- A review. Journal of Low Frequency Noise, Vibration and Active Control. [En línea].Vol. 40 (2), pp. 1005-1023. 22 de octubre de 2019. [Fecha de consulta: 12 de marzo de 2024]. DOI: 10.1177/1461348419876392 ISSN: 1461-3484.
6. PIÑÓN, Alejandro; Favela-Contreras, A., Félix-Herrán, L. C., Beltrán-Carvajal, F. y Lozoya, C. An ARX Model-Based Predictive Control of a Semi-Active Vehicle Suspension to Improve Passenger Comfort and Road-Holding. Actuators. [En línea]. Vol. 10 (3), pp. 1-17. 02 de marzo de 2021. [Fecha de consulta: 12 de marzo de 2024]. https://doi.org/10.3390/act10030047 ISSN: 2076-0825.
7. HUANG, Bin; Fu, X.,Wu, S. y Huang, S. Calculation Algorithm of Tire-Road Friction Coefficient Based on Limited-Memory Adaptive Extended Kalman Filter. Mathematical Problems in Engineering. [En línea]. 2019 (1), pp. 1-14. 2019. [Fecha de consulta: 12 de marzo de 2024]. https://doi.org/10.1155/2019/1056269 ISSN: 1563-5147.
8. JIANG, Bowen; Sharma, N., Liu, Y. y Li, Ch. Acceleration-based wheel slip control realized with decentralised electric drivetrain systems. IET Electrical Systems in Transportation. [En línea]. Vol. 12(2), pp. 143-152. Junio de 2022. [Fecha de consulta: 13 de marzo de 2024]. DOI:10.1049/els2.12044 ISSN: 2042-9746.
9. LENG, Bo; Jiang, Y. y Yu, Z. Distributed drive electric autonomous vehicle steering angle control based on active disturbance rejection control. Journal of Automobile Engineering. [En línea]. Vol. 235 (1), pp. 1-15. 06 de agosto de 2020. [Fecha de consulta: 13 de marzo de 2024]. https://doi.org/10.1177/0954407020944288 ISSN: 2041-2991.
10. ETIÉNNE, Lucien; Acosta, C., DiGennaro, S. y Barbot, J. P. A Super-twisting Controller for Active Control of Ground Vehicles with Lateral Tire-road Friction Estimation and CarSim Validation. International Journal of Control, Automation and Systems. [En línea]. Vol. 18, pp. 1177-1189. 05 de mayo de 2020. [Fecha de consulta: 13 de marzo de 2024]. DOI:10.1007/s12555-018-0484-0 ISSN: 1598-6446.
11. ZHANG, Jinhua; Sun, W. y Jing, H. Nonlinear Robust Control of Antilock Braking Systems Assisted by Active Suspensions for Automobile. IEEE Transactions on Control Systems Technology. [En línea]. Vol. 27 (3), pp. 1352-1359. Mayo de 2019. [Fecha de consulta: 14 de marzo de 2024]. DOI: 10.1109/TCST.2018.2810823 ISSN: 1063-6536.
12. GONG, Jianqiang; Luo, Y., Qiu, Z. y Wang, X. Determination of key components in automobile braking systems based on ABC classification and FMECA. Journal of Traffic and Transportation Engineering. [En línea]. Vol. 9 (1), pp. 69-77. Febrero de 2022. [Fecha de consulta: 14 de marzo de 2024]. DOI:10.1016/j.jtte.2019.01.008 ISSN: 2095-7564.
13. ZHANG, Junjiang; Yang, Y., Hu, M., Yang, Y. y Fu, Ch. Longitudinal–vertical comprehensive control for four-wheel drive pure electric vehicle considering energy recovery and ride comfort. Energy. [En línea]. Vol. 236 (1), pp. 12-17. Diciembre de 2021. [Fecha de consulta: 14 de marzo de 2024]. DOI:10.1016/j.energy.2021.121417. ISSN: 0360-5442.
14. LI, Panshuo; Lam, J. y Cheung, K. Ch. Motion-based active disturbance rejection control for a non-linear full-car suspension system. Journal of Automobile Engineering. [En línea]. Vol. 232 (5), pp. 1-16. 07 de agosto de 2017. [Fecha de consulta: 20 de marzo de 2024]. https://doi.org/10.1177/0954407017704781 ISSN: 2041-2991
15. QI, Hengmin; Chen, Y. y Tan, B. Improvement of both handling stability and ride comfort of a vehicle via coupled hydraulically interconnected suspension and electronic controlled air spring. Journal of Automobile Engineering. [En línea]. Vol. 234 (2-3), pp. 1-20. 2019. [Fecha de consulta: 20 de marzo de 2024]. https://doi.org/10.1177/0954407019856538 ISSN: 2041-2991.
16. NGUYEN, Tuan Anh. Improving the Comfort of the Vehicle Based on Using the Active Suspension System Controlled by the Double-Integrated Controller. Shock and Vibration. [En línea]. 2021, pp. 1-11. 06 de septiembre de 2021. [Fecha de consulta: 21 de marzo de 2024]. https://doi.org/10.1155/2021/1426003 ISSN: 1875-9203.
17. NAHIDI, Asal; Kazahiesadeh, A.,Khosravani, S., Khajepour, A., Chen, S. K. y Litkouhi, B. Modular integrated longitudinal and lateral vehicle stability control for electric vehicles. Mechatronics. [En línea]. Vol. 44, pp. 60-70. Junio de 2017. [Fecha de consulta: 22 de marzo de 2024]. https://doi.org/10.1016/j.mechatronics.2017.04.001 ISSN: 0957-4158.
18. LENZO, Basilio; Sorniotti, A., Gruber, P. y Sannen, K. On the experimental analysis of single input single output control of yaw rate and sideslip angle. International Journal of Automotive Technology. [En línea]. Vol. 18, pp. 799-811. 09 de julio de 2017. [Fecha de consulta: 22 de marzo de 2024]. DOI:10.1007/s12239-017-0079-4 ISSN: 1976-3832.
19. LENZO, Basilio; Zanchetta, M., Sorniotti, A., Gruber, P. y De Nijs, W. Yaw Rate and Sideslip Angle Control Through Single Input Single Output Direct Yaw Moment Control. IEEE Transactions on Control Systems Technology. [En línea]. Vol. 29 (1), pp. 124-139. Enero de 2021. [Fecha de consulta: 23 de marzo de 2024]. DOI: 10.1109/TCST.2019.2949539 ISSN: 1558-0865.
20. ZHOU, Hongliang; Jia, F., Jing, H., Liu, Z. y Güvenc, L. Coordinated Longitudinal and Lateral Motion Control for Four Wheel Independent Motor-Drive Electric Vehicle. IEEE Transactions on Vehicular Technology. [En línea]. Vol. 67 (5), pp. 3782-3790. Mayo de 2018. [Fecha de consulta: 23 de marzo de 2024]. DOI: 10.1109/TVT.2018.2816936 ISSN: 1939-9359.
21. XIE, Xianyi; Jin, L., Jiang, Y. y Guo, B. Integrated Dynamics Control System With ESC and RAS for a Distributed Electric Vehicle. IEEE Access. [En línea]. Vol. 6, pp. 18694-18704. 02 de abril de 2018. [Fecha de consulta: 24 de marzo de 2024]. DOI: 10.1109/ACCESS.2018.2819206 ISSN: 2169-3536
22. TOTA, Antonio; Lenzo, B., Lu, Q., Sorniotti, A. Gruber, P., Fallah, S., Velardocchia, E. G. y De Smet, J. On the Experimental Analysis of Integral Sliding Modes for Yaw Rate and Sideslip Control of an Electric Vehicle with Multiple Motors. International Journal of Automotive Technology. [En línea],. Vol. 19 (5), pp. 811−823. 12 de septiembre de 2018. [Fecha de consulta: 25 de marzo de 2024]. DOI: https://doi.org/10.1007/s12239-018-0078-0 ISSN: 1976-3832.
23. ATAEI, Mansour; Khajepour, A. y Jeon, S. Model Predictive Control for integrated lateral stability, traction/braking control, and rollover prevention of electric vehicles. Vehicle System Dynamics. [En línea]. Vol. 58 (1), pp. 49-73. 2020. [Fecha de consulta: 25 de marzo de 2024]. https://doi.org/10.1080/00423114.2019.1585557 ISSN: 0042-3114.
24. YIN, Dejun; Sun, N. y Hu, J. S. A Wheel Slip Control Approach Integrated With Electronic Stability Control for Decentralized Drive Electric Vehicles. IEEE Transactions on Industrial Informatics. [En línea]. Vol. 15 (4), pp. 2244-2252. Abril de 2019. [Fecha de consulta: 25 de marzo de 2024]. DOI: 10.1109/TII.2019.2895371 ISSN: 1557-9948.
25. ASIABAR, Aria Noori y Kazemi, Reza. A direct yaw moment controller for a four in-wheel motor drive electric vehicle using adaptive sliding mode control. Journal of Multi-body Dynamics. [En línea]. Vol. 233 (3), pp. 1-19. Septiembre de 2019. [Fecha de consulta: 26 de marzo de 2024]. https://doi.org/10.1177/1464419318807700 ISSN: 1464-4193.
26. TAHOUNI, Amin; Mirzaei, M. y Najjari, B. Novel Constrained Nonlinear Control of Vehicle Dynamics Using Integrated Active Torque Vectoring and Electronic Stability Control. IEEE Transactions on Vehicular Technology. [En línea]. Vol. 68 (10), pp. 9564-9572. Octubre de 2019. [Fecha de consulta: 26 de marzo de 2024]. DOI: 10.1109/TVT.2019.2933229 ISSN: 1939-9359.
27. SUN, Peikun; Stensson, A., Drugge, L. y Jerrelind, J. Energy efficiency and stability of electric vehicles utilising direct yaw moment control. Vehicle System Dynamics. [En línea]. Vol. 60 (3), pp. 930-950. 17 de noviembre de 2020. [Fecha de consulta: 27 de marzo de 2024]. DOI:10.1080/00423114.2020.1841903 ISSN: 0042-3114.
28. VIGNATI, M. y Sabbioni, E. A cooperative control strategy for yaw rate and sideslip angle control combining torque vectoring with rear wheel steering. Vehicle System Dynamics. [En línea]. Vol. 60 (5), pp. 1668-1701. 2022. [Fecha de consulta: 27 de marzo de 2024]. DOI:10.1080/00423114.2020.1869273 ISSN: 0042-3114.
29. AHMADIAN, Narjes; Khosravi, A. y Sarhadi, P. Driver assistant yaw stability control via integration of AFS and DYC. Vehicle System Dynamics. [En línea]. Vol. 60 (5), pp. 1742-1762. 28 de enero de 2021. [Fecha de consulta: 28 de marzo de 2024]. https://www.tandfonline.com/doi/abs/10.1080/00423114.2021.1879390 ISSN: 0042-3114.
30. HUANG, Juhua; Liu, Y., Liu, M., Cao, M. y Yan, Q. Multi-Objective Optimization Control of Distributed Electric Drive Vehicles Based on Optimal Torque Distribution. IEEE Access. [En línea]. Vol. 7 (1), pp. 16377-16394. 22 de enero de 2019. [Fecha de consulta: 28 de marzo de 2024]. DOI: 10.1109/ACCESS.2019.2894259 ISSN: 2169-3536
31. HU, Jianjun; Tao, J., Xiao, F., Niu, X. y Fu, Ch. An Optimal Torque Distribution Control Strategy for Four-Wheel Independent Drive Electric Vehicles Considering Energy Economy. IEEE Access. [En línea]. Vol. 7 (1), pp. 141826-141837. 30 de septiembre de 2019. [Fecha de consulta: 29 de marzo de 2024]. DOI: 10.1109/ACCESS.2019.2944479 ISSN: 2169-3536.
32. Al-Fiky, Hossam T., Asfoor, M. S., Yacoob, M. I. y Sharaf, A. M. Electronic Differential Optimization for Electric Vehicle Full Model for In-Wheel Permanent Magnet Brushless DC Motors. IEEE 2019 7th International Conference on Control, Mechatronics and Automation (ICCMA). [En línea]. pp. 15-20. 6-8 de noviembre de 2019. Delft, Holanda. [Fecha de consulta: 29 de marzo de 2024]. DOI: 10.1109/ICCMA46720.2019.8988695
33.GUO, Luole; Xu, H. y Zou, J. Acceleration slip regulation control strategy for four-wheel independent drive electric vehicles. IEEJ Transactions on Electrical and Electronic Engineering. [En línea]. Vol. 14 (4), pp. 630-639. Abril de 2019. [Fecha de consulta: 30 de marzo de 2024]. https://doi.org/10.1002/tee.22846 ISSN:1931-4981.
34. PARRA, Alberto; Zubizarreta, A. y Pérez, J. An energy efficient intelligent torque vectoring approach based on fuzzy logic controller and neural network tire forces estimator. Neural Computing and Applications. [En línea]. Vol. 33 (15), pp. 9171–9184. 13 de enero de 2021. [Fecha de consulta: 30 de marzo de 2024]. DOI:10.1007/s00521-020-05680-2 ISSN:1433-3058.
35. WANG, Junnian; Wang, X., Luo, Z. y Assadian, F. Active Disturbance Rejection Control of Differential Drive Assist Steering for Electric Vehicles. Energies. [En línea]. Vol. 13 (10), pp. 1-22. 22 de mayo de 2020. [Fecha de consulta: 31 de marzo de 2024]. https://doi.org/10.3390/en13102647 ISSN: 1996-1073.
36. Rajamani, Rajesh. Vehicle Dynamics and Control. New York: Springer. 2006. 497 pp. ISBN: 9780387263960.
37. CHENG, Shuo; Mei, M., Ran, X., Li, L. y Zhao, L. Adaptive Unified Monitoring System Design for Tire-Road Information. Journal of Dynamic Systems, Measurement, and Control. [En línea]. Vol. 141 (7), pp. 1-11. Julio de 2019. [Fecha de consulta: 31 de marzo de 2024]. https://doi.org/10.1115/1.4043113 ISSN: 0022-0434.
38. ACOSTA, Cuauhtémoc y Di Gennaro, S. Nonlinear adaptive tracking for ground vehicles in the presence of lateral wind disturbance and parameter variations. Journal of the Franklin Institute. [En línea]. Vol. 354 (7), pp. 2742-2768. Mayo de 2017. [Fecha de consulta: 31 de marzo de 2024]. https://doi.org/10.1016/j.jfranklin.2017.01.020 ISSN: 1879-2693.
39. Pacejka, Hans B. Tyre and Vehicle Dynamics. Segunda edición. Reino Unido. Elsevier. 2006. 657 pp. ISBN-10: 0-7506-6918-7.
40. ZOU, Yuan; Guo, N. y Zhang, X. An integrated control strategy of path following and lateral motion stabilization for autonomous distributed drive electric vehicles. Journal of Automobile Engineering. [En línea]. Vol. 235 (4), pp. 1-16. 13 de noviembre de 2019. [Fecha de consulta: 01 de abril de 2024]. https://doi.org/10.1177/0954407019884168 ISSN: 2041-2991.
41. GUO, Jinghua; Wang, J., Luo, Y. y Li, K. Robust lateral control of autonomous four-wheel independent drive electric vehicles considering the roll effects and actuator faults. Mechanical Systems and Signal Processing. [En línea]. Vol. 143 (1), pp. 1-17. Septiembre de 2020. [Fecha de consulta: 01 de abril de 2024]. https://doi.org/10.1016/j.ymssp.2020.106773 ISSN: 0888-3270.
42. AO, Di; Li, J., Zhang, L. y Hong, J. Advanced post-impact safety and stability control for electric vehicles. IET Intelligent Transport Systems. [En línea]. Vol. 16 (12), pp. 1753-1767. Diciembre de 2022. [Fecha de consulta: 01 de abril de 2024]. https://doi.org/10.1049/itr2.12230 ISSN: 1751-9578.
43. SANDOVAL, Sergio; González, J. M., Jiménez, R., Villavazo, E., Molina., J. E., Sánchez, M. G. y Ochoa, V. J. A Low-Cost Platform for Modeling and Controlling the Yaw Dynamics of an Agricultural Tractor to Gain Autonomy. Electronics. [En línea]. Vol. 9 (11), pp. 1-20. 2 de noviembre de 2020. [Fecha de consulta: 01 de abril de 2024]. https://doi.org/10.3390/electronics9111826 ISSN: 2079-9292.